题目内容
已知△OAB三顶点坐标分别是O(0,0)、A(1,1)、B(2,0),直线ax+by=1与线段OA、AB都有公共点,则对于2a-b下列叙述正确的是( )A.有最大值而无最小值
B.有最小值而无最大值
C.既有最大值也有最小值
D.既无最大值也无最小值
【答案】分析:根据所给的三个点的坐标和直线与两条直线都有公共点,得到关于a,b的不等式组,根据不等式组画出可行域,则目标函数z=2a-b的最值情况可知.
解答:解:由O(0,0)、A(1,1)、B(2,0),因为直线ax+by=1与线段OA有公共点,所以-1×(a+b-1)≤0,
即a+b-1≥0,又直线ax+by=1与线段AB有公共点,则(a+b-1)(2a-1)≤0,因为a+b-1≥0,所以2a-1≤0.
由此得不等式组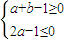 .
.
令z=2a-b,
画出不等式组表示的平面区域,如图,
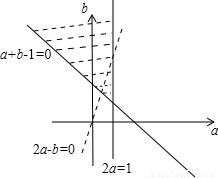
判断知,z=2a-b有最大值无最小值.
故选A.
点评:本题考查线性规划的应用,本题解题的关键是写出约束条件,表示出目标函数,画出可行域,得到最优解,本题是一个基础题.
解答:解:由O(0,0)、A(1,1)、B(2,0),因为直线ax+by=1与线段OA有公共点,所以-1×(a+b-1)≤0,
即a+b-1≥0,又直线ax+by=1与线段AB有公共点,则(a+b-1)(2a-1)≤0,因为a+b-1≥0,所以2a-1≤0.
由此得不等式组
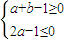 .
.令z=2a-b,
画出不等式组表示的平面区域,如图,

判断知,z=2a-b有最大值无最小值.
故选A.
点评:本题考查线性规划的应用,本题解题的关键是写出约束条件,表示出目标函数,画出可行域,得到最优解,本题是一个基础题.

练习册系列答案
相关题目
已知△OAB三顶点坐标分别是O(0,0)、A(1,1)、B(2,0),直线ax+by=1与线段OA、OB都有公共点,则对于z=2a-b,下列叙述正确的是 ( )
| A、有最大值2 | ||
| B、有最小值2 | ||
| C、没有最大值 | ||
D、有最小值
|

