题目内容
已知各项均为非负整数的数列A0∶a0,a1,…,an(n∈N*),满足a0=0,a1+…+an=n.若存在最小的正整数k,使得ak=k(k≥1),则可定义变换T,变换T将数列A0变为T(A0)∶a0+1,a1+1,…,ak-1+1,0,ak+1,…,an.设Ai+1=T(Ai),i=0,1,2….
(Ⅰ)若数列A0:0,1,1,3,0,0,试写出数列A5;若数列A4:4,0,0,0,0,试写出数列A0;
(Ⅱ)证明存在数列A0,经过有限次T变换,可将数列A0变为数列![]() ;
;
(Ⅲ)若数列A0经过有限次T变换,可变为数列![]() .设Sm=am+am+1+…+an,m=1,2,…,n,求证am=Sm-[
.设Sm=am+am+1+…+an,m=1,2,…,n,求证am=Sm-[![]() ](m+1),其中[
](m+1),其中[![]() ]表示不超过
]表示不超过![]() 的最大整数.
的最大整数.
答案:

练习册系列答案
相关题目
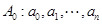
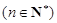 ,满足
,满足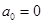 ,
,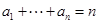 .若存在最小的正整数
.若存在最小的正整数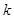 ,使得
,使得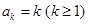 ,则可定义变换
,则可定义变换 ,变换
,变换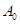 变为数列
变为数列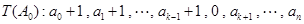 .设
.设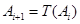 ,
,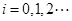 .
.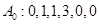 ,试写出数列
,试写出数列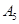 ;若数列
;若数列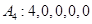 ,试写出数列
,试写出数列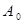 ;
;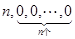 ;
;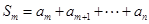 ,
,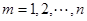 ,求证
,求证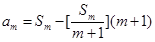 ,其中
,其中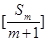 表示不超过
表示不超过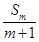 的最大整数.
的最大整数.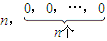 ;
;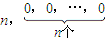 .设Sm=am+am+1+…+an,m=1,2,…,n,求证
.设Sm=am+am+1+…+an,m=1,2,…,n,求证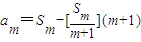 ,其中
,其中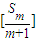 表示不超过
表示不超过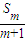 的最大整数.
的最大整数. ;
; .设Sm=am+am+1+…+an,m=1,2,…,n,求证
.设Sm=am+am+1+…+an,m=1,2,…,n,求证 ,其中
,其中 表示不超过
表示不超过 的最大整数.
的最大整数.