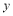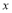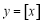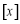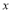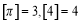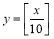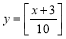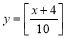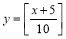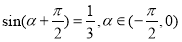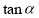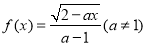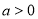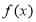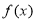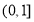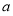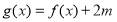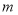题目内容
已知函数 过点
过点 .
.
(1)求实数 ;
;
(2)将函数 的图像向下平移1个单位,再向右平移
的图像向下平移1个单位,再向右平移 个单位后得到函数
个单位后得到函数 图像,设函数
图像,设函数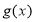 关于
关于 轴对称的函数为
轴对称的函数为 ,试求
,试求 的解析式;
的解析式;
(3)对于定义在 上的函数
上的函数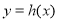 ,若在其定义域内,不等式
,若在其定义域内,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(1)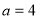 ;(2)
;(2)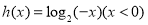 ;(3)
;(3)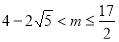 .
.
【解析】
试题分析:(1)由条件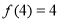 即可解出
即可解出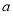 ;(2)函数
;(2)函数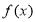 向下平移1个单位得到
向下平移1个单位得到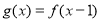 ,然后关于
,然后关于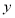 轴对称得到
轴对称得到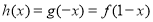 ,代入(1)式的
,代入(1)式的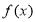 即可得到函数
即可得到函数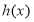 的解析式;(3)设
的解析式;(3)设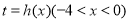 ,故
,故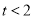 ,将不等式
,将不等式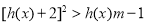 在其定义域恒成立的问题,转化二次函数
在其定义域恒成立的问题,转化二次函数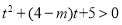 在
在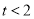 时恒成立,然后根据二次函数的图像与性质进行求解即可得到
时恒成立,然后根据二次函数的图像与性质进行求解即可得到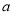 的取值范围.
的取值范围.
试题解析:(1)由已知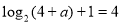 ,
,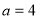 3分
3分
(2)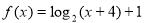 向下平移个单位后再向右平移
向下平移个单位后再向右平移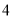 个单位后得到函数
个单位后得到函数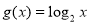 ,函数
,函数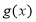 关于
关于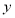 轴对称的函数为
轴对称的函数为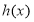
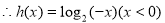 6分
6分
(3)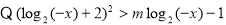 在
在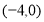 恒成立
恒成立
 设
设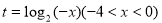 则
则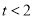
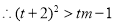 即:
即: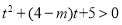 ,在
,在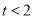 时恒成立 8分
时恒成立 8分
令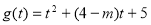


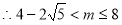 11分
11分
或
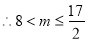 13分
13分
综合得: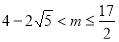 14分.
14分.
考点:1.对数函数的图像与性质;2.函数图像的平移与对称变换;3.二次函数的最值问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目