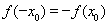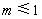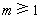题目内容
对于函数 ,若存在实数
,若存在实数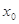 ,使
,使 成立,则称
成立,则称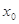 为
为 的不动点.
的不动点.
⑴当 时,求
时,求 的不动点;
的不动点;
⑵若对于任何实数 ,函数
,函数 恒有两相异的不动点,求实数
恒有两相异的不动点,求实数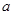 的取值范围;
的取值范围;
⑶在⑵的条件下,若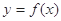 的图象上A、B两点的横坐标是函数
的图象上A、B两点的横坐标是函数 的不动点,且直线
的不动点,且直线 是线段AB的垂直平分线,求实数b的取值范围.
是线段AB的垂直平分线,求实数b的取值范围.
【答案】

(1) 的不动点是-1,2.
的不动点是-1,2.
(2)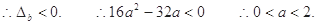 (3)0>
(3)0>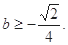
【解析】(1)设x为不动点,则有2x2-x-4=x,变形为2x2-2x-4=0,解方程即可.
(2)将f(x)=x转化为ax2+bx+b-2=0.由已知,此方程有相异二实根,则有△x>0恒成立求解;
(3)由垂直平分线的定义解决,由A、B两点的横坐标是函数f(x)的不动点,则有kAB=1,再由直线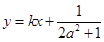 是线段AB的垂直平分线,得到k=-1,再由中点在直线
是线段AB的垂直平分线,得到k=-1,再由中点在直线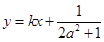 上求解.
上求解.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目