题目内容
如图,四棱锥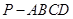 的底面
的底面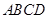 为矩形,且
为矩形,且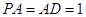 ,
,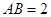 ,
,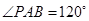 ,
,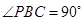 ,
,
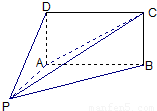
(Ⅰ)平面PAD与平面PAB是否垂直?并说明理由;
(Ⅱ)求直线PC与平面ABCD所成角的正弦值.
【答案】
(Ⅰ)垂直;(Ⅱ)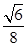 .
.
【解析】
试题分析:(Ⅰ)由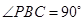 得
得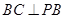 ,由底面
,由底面 为矩形得
为矩形得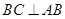 ,从而有
,从而有 ⊥平面
⊥平面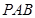 .而
.而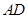 ∥
∥ ,所以
,所以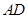 ⊥平面
⊥平面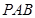 ,再由线面垂直的性质得平面
,再由线面垂直的性质得平面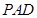 ⊥平面
⊥平面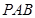 ;(Ⅱ)过点
;(Ⅱ)过点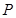 作
作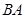 延长线的垂线
延长线的垂线 ,垂足为
,垂足为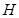 ,连接
,连接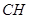 .然后可以证明
.然后可以证明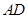 ⊥平面
⊥平面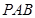 ,从而
,从而 为
为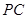 与底面
与底面 所成的角.然后根据相关数据得到直角三角形
所成的角.然后根据相关数据得到直角三角形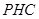 各边长,最后得到直线
各边长,最后得到直线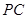 与平面
与平面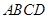 所成角的正弦值为
所成角的正弦值为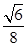 .
.
试题解析:(Ⅰ)平面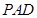 ⊥平面
⊥平面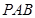
∵ ∴
∴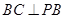
∵四棱锥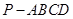 的底面
的底面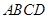 为矩形 ∴
为矩形 ∴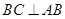
∵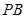 ⊂平面
⊂平面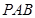 ,
,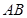 ⊂平面
⊂平面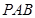 ,且
,且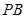 ∩
∩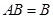 ∴
∴ ⊥平面
⊥平面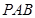 (4分)
(4分)
∵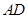 ∥
∥ ∴
∴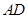 ⊥平面
⊥平面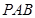 ∵
∵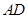 ⊂平面
⊂平面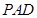
平面 ⊥平面
⊥平面 (6分)
(6分)
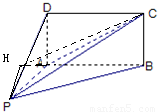
(Ⅱ)如图,过点 作
作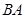 延长线的垂线
延长线的垂线 ,垂足为
,垂足为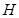 ,连接
,连接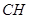 .
.
由(Ⅰ)可知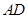 ⊥平面
⊥平面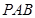
∵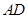 ⊂平面
⊂平面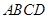
∴平面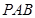 ⊥平面
⊥平面
∵ ⊂平面
⊂平面 ,平面
,平面 ⊥平面
⊥平面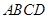 ,
,
平面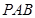 ∩平面
∩平面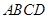 =
=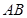
∴ ⊥平面
⊥平面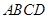
∴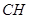 为
为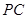 在平面
在平面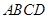 内的射影.
内的射影.
∴ 为
为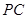 与底面
与底面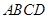 所成的角.
(9分)
所成的角.
(9分)
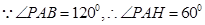 ,
,
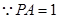 ,
,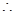 在直角三角形
在直角三角形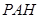 中,
中,
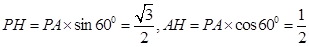
在直角三角形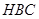 中,
中,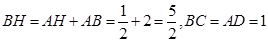
故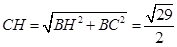
在直角三角形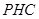 中,
中,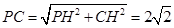 ,
,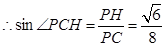
故直线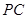 与平面
与平面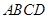 所成角的正弦值
所成角的正弦值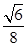 .
(12分)
.
(12分)
考点:1.线面垂直的判定与性质;2.直线与平面所成的角.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
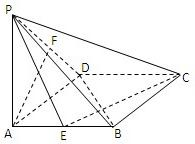 如图,四棱锥的底面为菱形,PA⊥底面ABCD,E、F分别是AB与PD的中点.
如图,四棱锥的底面为菱形,PA⊥底面ABCD,E、F分别是AB与PD的中点. 如图,四棱锥
如图,四棱锥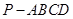 的底面
的底面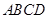 为矩形,且
为矩形,且 ,
,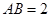 ,
, ,
,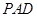
 平面
平面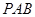 ;
;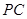 与平面
与平面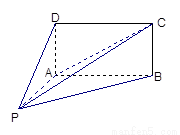
 的底面
的底面 为菱形,
为菱形, 平面
平面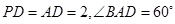 ,
, 、
、 分别为
分别为 、
、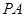 的中点。
的中点。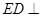 平面
平面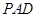 ;
; (Ⅱ)求三棱锥
(Ⅱ)求三棱锥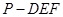 的体积;
的体积;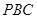 所成的锐二面角大小的余弦值。
所成的锐二面角大小的余弦值。