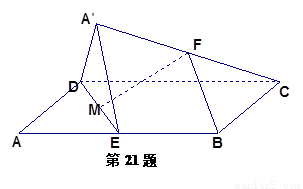
题目内容
如图,在平行四边形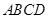 中,
中,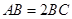 ,
,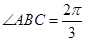 ,
,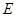 为线段
为线段 的中线,将△
的中线,将△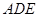 沿直线
沿直线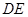 翻折成△
翻折成△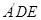 ,使平面
,使平面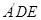 ⊥平面
⊥平面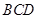 ,
,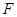 为线段
为线段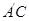 的中点.
的中点.
(1)求证: ∥平面
∥平面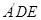 ;
;
(2)设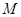 为线段
为线段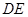 的中点,求直线
的中点,求直线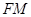 与平面
与平面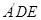 所成角的余弦值.
所成角的余弦值.
【答案】
(1)证明:取A′D的中点G,连结GF,CE,由条件易知
FG∥CD,FG=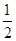 CD.
CD.
BE∥CD,BE=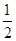 CD.
CD.
所以FG∥BE,FG=BE.
故四边形BEGF为平行四边形,
所以BF∥EG
 因为
因为 平面
平面 ,BF
,BF 平面
平面
所以 BF//平面
(2)解:在平行四边形,ABCD中,设BC=a
则AB=CD=2a, AD=AE=EB=a,
连CE,因为
在△BCE中,可得CE=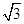 a,
a,
在△ADE中,可得DE=a,
在△CDE中,因为CD2=CE2+DE2,所以CE⊥DE,
在正三角形A′DE中,M为DE中点,所以A′M⊥DE.
由平面A′DE⊥平面BCD,
可知A′M⊥平面BCD,A′M⊥CE.
取A′E的中点N,连线NM、NF,
所以NF⊥DE,NF⊥A′M.
因为DE交A′M于M,
所以NF⊥平面A′DE,
则∠FMN为直线FM与平面A′DE新成角.
在Rt△FMN中,NF=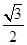 a, MN=
a, MN=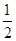 a, FM=a,
a, FM=a,
则cos =
=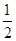 .
.
所以直线FM与平面A′DE所成角的余弦值为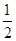
【解析】略

练习册系列答案
相关题目


 中,
中, ,将
,将 沿
沿 折起到
折起到 的位置,使平面
的位置,使平面 平面
平面 .
. 的表面积和体积.
的表面积和体积.
 中,已知
中,已知 ,
, ,
, ,
, 为
为 的中点,则
的中点,则

 中,设
中,设 ,
, ,
, 为边
为边 的中点,则
的中点,则

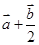 B.
B.

 D.
D.
