题目内容
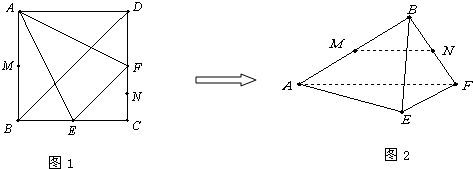
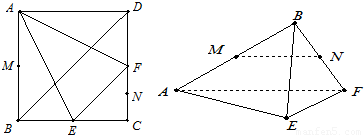
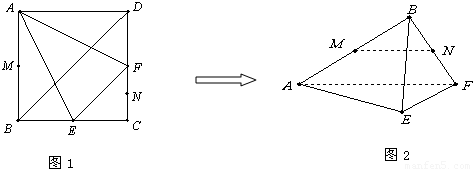
 在边长为4cm的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合,重合后的点记为B,构成一个三棱锥.
在边长为4cm的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合,重合后的点记为B,构成一个三棱锥.(1)请判断MN与平面AEF的位置关系,并给出证明;
(2)证明AB⊥平面BEF;
(3)求二面角M-EF-B的余弦值.
分析:(1)由题意及图形的翻折规律可知MN应是△ABF的一条中位线,利用线面平行的判定定理即可求证;
(2)根据翻折前AB⊥BE,AD⊥DF,可知翻折后AB⊥BE,AB⊥BF,结合线面垂直的判定定理得到AB⊥平面BEF;
(3)记EF的中点为G,连接MF,BG,MG,可得∠MGB是二面角M-EF-B的平面角,解△MGB,可得二面角M-EF-B的余弦值
(2)根据翻折前AB⊥BE,AD⊥DF,可知翻折后AB⊥BE,AB⊥BF,结合线面垂直的判定定理得到AB⊥平面BEF;
(3)记EF的中点为G,连接MF,BG,MG,可得∠MGB是二面角M-EF-B的平面角,解△MGB,可得二面角M-EF-B的余弦值
解答:(1)解:MN∥平面AEF…(1分)
证明如下:因M、N分别为AB、CF的中点,
翻折后B、C、D重合,
∴MN是△ABF的一条中位线,…(3分)
∴MN∥AF
又∵MN?平面AEF,AF?平面AEF
∴MN∥平面AEF.…(6分)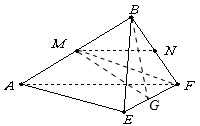
(2)证明:∵正方形ABCD中,AB⊥BE,AD⊥DF,
∴翻折后AB⊥BE,AB⊥BF,
又∵BE∩BF=B,BE,BF?平面BEF
∴AB⊥平面BEF,…(8分)
(3)记EF的中点为G,连接MF,BG,MG
∵BE=BF,ME=MF
∴BG⊥EF且MG⊥EF,
故∠MGB是二面角M-EF-B的平面角…10分
∵AB⊥平面BEF
∴∠MBG=90°
在△BEF中,BG=
,
又由MB=2,
∴MG=
=
∴cos∠MGB=
=
即二面角M-EF-B的余弦值
…12分
证明如下:因M、N分别为AB、CF的中点,
翻折后B、C、D重合,
∴MN是△ABF的一条中位线,…(3分)
∴MN∥AF
又∵MN?平面AEF,AF?平面AEF
∴MN∥平面AEF.…(6分)

(2)证明:∵正方形ABCD中,AB⊥BE,AD⊥DF,
∴翻折后AB⊥BE,AB⊥BF,
又∵BE∩BF=B,BE,BF?平面BEF
∴AB⊥平面BEF,…(8分)
(3)记EF的中点为G,连接MF,BG,MG
∵BE=BF,ME=MF
∴BG⊥EF且MG⊥EF,
故∠MGB是二面角M-EF-B的平面角…10分
∵AB⊥平面BEF
∴∠MBG=90°
在△BEF中,BG=
| 2 |
又由MB=2,
∴MG=
| MB2+BG2 |
| 6 |
∴cos∠MGB=
| BG |
| MG |
| ||
| 3 |
即二面角M-EF-B的余弦值
| ||
| 3 |
点评:本题考查线面平行,线面垂直,考查二面角的平面角的计算,掌握线面平行,线面垂直的判定方法及二面角平面角的构造是关键.

练习册系列答案
相关题目