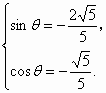题目内容
已知偶函数f(x)=cos![]() sinx-sin(x-
sinx-sin(x-![]() )+(tan
)+(tan![]() -2)sinx-sin
-2)sinx-sin![]() 的最小值是0,求f(x)的最大值及此时x的集合.
的最小值是0,求f(x)的最大值及此时x的集合.
答案:
解析:
解析:
|
解:f(x)=cos =sin 因为f(x)是偶函数, 所以对任意xÎ R,都有f(-x)=f(x), 即sin 即(tan 所以tan 由 此时,f(x)=sin 当sinq
= 当sinq
= 当cosx=-1时,f(x)有最大值为 自变量x的集合为{x|x=2kp +p ,kÎ Z}. |

练习册系列答案
相关题目
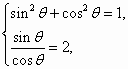 解得
解得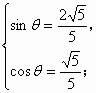 或
或