题目内容
(1)已知函数y=ln(-x2+x-a)的定义域为(-2,3),求实数a的取值范围;
(2)已知函数y=ln(-x2+x-a)在(-2,3)上有意义,求实数a的取值范围.
(1)-6 (2)a≤-6
解析试题分析:(1)因为,函数y=ln(-x2+x-a)的定义域为(-2,3),所以,-x2+x-a>0的解集为(-2,3),-2,3是方程-x2+x-a=0的根,故a=-6。
(2)因为,函数y=ln(-x2+x-a)在(-2,3)上有意义,即-x2+x-a>0在(-2,3)成立,而二次函数-x2+x-a的图象开口向下,对称轴为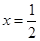 ,所以,-32+3-a
,所以,-32+3-a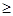 0,故a≤-6。
0,故a≤-6。
考点:对数函数的性质,一元二次不等式的解法,二次函数的图象和性质。
点评:中档题,本题以对比的形式,给出在不同要求下,此类问题的解法,同时注重了基础性。对于一元二次问题,往往借助于二次函数的图象和性质,数形结合。

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
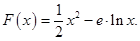
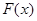 的极值;
的极值;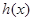 和
和 定义域内的任意实数
定义域内的任意实数 ,若存在常数
,若存在常数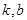 ,使得不等式
,使得不等式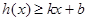 和
和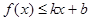 都成立,则称直线
都成立,则称直线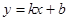 是函数
是函数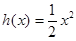 ,
,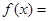
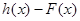 ,试问函数
,试问函数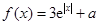 (
(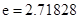 是自然对数的底数)的最小值为
是自然对数的底数)的最小值为 .
. 的值;
的值;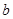
 且
且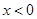 ,试解关于
,试解关于 的不等式
的不等式 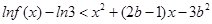 ;
;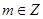 且
且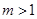 .若存在实数
.若存在实数 ,使得对任意的
,使得对任意的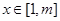 ,都有
,都有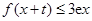 ,试求
,试求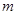 的最大值.
的最大值.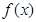 是二次函数,不等式
是二次函数,不等式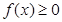 的解集为
的解集为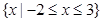 ,且
,且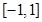 上的最小值是4.
上的最小值是4. ,若对任意的
,若对任意的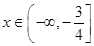 ,
, 均成立,求实数
均成立,求实数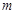 的取值范围.
的取值范围. 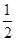 ,用水越多洗掉的农药量也越多,但总还有农药残留在蔬菜上.设用
,用水越多洗掉的农药量也越多,但总还有农药残留在蔬菜上.设用 单位量的水清洗一次以后,蔬菜上残留的农药量与本次清洗前残留的农药量之比为函数
单位量的水清洗一次以后,蔬菜上残留的农药量与本次清洗前残留的农药量之比为函数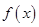 .
.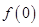 的值,并解释其实际意义;
的值,并解释其实际意义;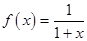 ,现有
,现有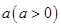 单位量的水,可以清洗一次,也可以把水平均分成两份后清洗两次.试问用那种方案清洗后蔬菜上残留的农药量比较少?说明理由.
单位量的水,可以清洗一次,也可以把水平均分成两份后清洗两次.试问用那种方案清洗后蔬菜上残留的农药量比较少?说明理由.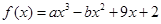 ,若f(x)在x=1处的切线方程为3x+y-6=0
,若f(x)在x=1处的切线方程为3x+y-6=0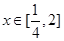 ,都有f(x)
,都有f(x)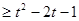 成立,求函数g(t)
成立,求函数g(t)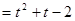 的最值
的最值 万元满足
万元满足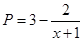 ,已知生产该产品还需投入成本
,已知生产该产品还需投入成本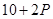 万元(不含促销费用),产品的销售价格定为
万元(不含促销费用),产品的销售价格定为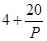 元.
元.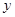 万元表示为促销费用
万元表示为促销费用 亿元,其中用于风景区改造为
亿元,其中用于风景区改造为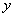 亿元。该市决定建立生态环境改造投资方案,该方案要求同时具备下列三个条件:①每年用于风景区改造费用随每年改造生态环境总费用增加而增加;②每年改造生态环境总费用至少
亿元。该市决定建立生态环境改造投资方案,该方案要求同时具备下列三个条件:①每年用于风景区改造费用随每年改造生态环境总费用增加而增加;②每年改造生态环境总费用至少 亿元,至多
亿元,至多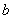 亿元;③每年用于风景区改造费用不得低于每年改造生态环境总费用的15%,但不得每年改造生态环境总费用的22%。
亿元;③每年用于风景区改造费用不得低于每年改造生态环境总费用的15%,但不得每年改造生态环境总费用的22%。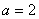 ,
,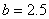 ,请你分析能否采用函数模型y=
,请你分析能否采用函数模型y=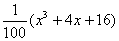 作为生态环境改造投资方案;
作为生态环境改造投资方案;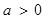 ,函数
,函数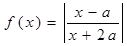 。
。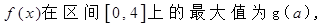 求
求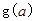 的表达式;
的表达式;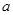 ,使函数
,使函数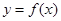 在区间
在区间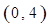 内的图像上存在两点,在该两点处的切线相互垂直?若存在,求
内的图像上存在两点,在该两点处的切线相互垂直?若存在,求