题目内容
(05年浙江卷理)(14分)
如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥底面ABC.
(Ⅰ)求证:OD∥平面PAB;
(Ⅱ)当k=![]() 时,求直线PA与平面PBC所成角的大小;
时,求直线PA与平面PBC所成角的大小;
(Ⅲ) 当k取何值时,O在平面PBC内的射影恰好为△PBC的重心?

解析:解法一
(Ⅰ)∵O、D分别为AC、PC的中点:∴OD∥PA,又AC![]() 平面PAB,∴OD∥平面PAB.
平面PAB,∴OD∥平面PAB.
(Ⅱ)∵AB⊥BC,OA=OC,∴OA=OC=OB,又∵OP⊥平面ABC,∴PA=PB=PC.
取BC中点E,连结PE,则BC⊥平面POE,作OF⊥PE于F,连结DF,则OF⊥平面PBC
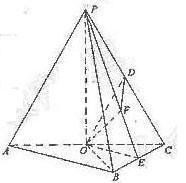
∴∠ODF是OD与平面PBC所成的角.
又OD∥PA,∴PA与平面PBC所成角的大小等于∠ODF.
在Rt△ODF中,sin∠ODF=![]() ,∴PA与平面PBC所成角为arcsin
,∴PA与平面PBC所成角为arcsin![]()
(Ⅲ)由(Ⅱ)知,OF⊥平面PBC,∴F是O在平面PBC内的射影.
∵D是PC的中点,若F是△PBC的重心,则B、F、D三点共线,直线OB在平面PBC内的射影为直线BD,∵OB⊥PC.∴PC⊥BD,∴PB=BC,即k=1..反之,,当k=1时,三棱锥O-PBC为正三棱锥,∴O在平面PBC内的射影为△PBC的重心.
解法二:
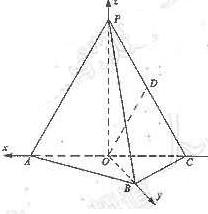
∵OP⊥平面ABC,OA=OC,AB=BC,∴OA⊥OB,OA⊥OP,OB⊥OP.
以O为原点,射线OP为非负x轴,建立空间坐标系O-xyz如图),设AB=a,则A(![]() a,0,0).
a,0,0).
B(0, ![]() a,0),C(-
a,0),C(-![]() a,0,0).设OP=h,则P(0,0,h).
a,0,0).设OP=h,则P(0,0,h).
(Ⅰ)∵D为PC的中点,∴![]() 又
又![]() ∥
∥![]() ,
,
∴OD∥平面PAB.
(Ⅱ)∵k=![]() 则PA=2a,∴h=
则PA=2a,∴h=![]() ∴
∴![]() 可求得平面PBC的法向量
可求得平面PBC的法向量![]()
∴cos![]() .
.
设PA与平面PBC所成角为θ,刚sinθ=|cos(![]() )|=
)|=![]() .
.
∴PA与平面PBC所成的角为arcsin![]() .
.
(Ⅲ)△PBC的重心G(![]() ),∴
),∴![]() =(
=(![]() ).
).
∵OG⊥平面PBC,∴![]() 又
又![]() ∴
∴![]() ,
,
∴h=![]() ,∴PA=
,∴PA=![]() ,即k=1,反之,当k=1时,三棱锥O-PBC为正三棱锥.
,即k=1,反之,当k=1时,三棱锥O-PBC为正三棱锥.
∴O为平面PBC内的射影为△PBC的重心.

 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案