题目内容
已知以下函数：（1）f（x）=3lnx；（2）f（x）=3ecosx；（3）f（x）=3ex；（4）f（x）=3cosx．
其中对于f（x）定义域内的任意一个自变量x1，都存在唯一一个自变量x2使
=3成立的函数是（ ）
其中对于f（x）定义域内的任意一个自变量x1，都存在唯一一个自变量x2使
| f(x1)f(x2) |
| A、（1）（2）（4） |
| B、（2）（3） |
| C、（3） |
| D、（4） |
分析：本题是选择题，可采用逐一检验的方法进行判定，抓住两个关键词“任意”与“唯一”进行判定．
解答：解：对于（1）
=3即lnx1•lnx2=1，而当x1=1时就不存在x2使之成立，故不符合
（2）
=3即cosx1+cosx2=0，当x1任取一值时，存在无数个x2使之成立，故不符合
（3）符合题意
（4）
=3即cosx1•cosx2=1当x1任取一值时，存在无数个x2使之成立，故不符合
故选C
| 3lnx1•3lnx2 |
（2）
| 3ecosx1• 3ecosx2 |
（3）符合题意
（4）
| 3cosx1•3cosx2 |
故选C
点评：本题考查了函数是否满足限制条件的函数问题，有一定的难度，属于中档题．
练习册系列答案
全能测控期末小状元系列答案
相关题目
成立的函数是（ ）
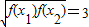成立的函数是（ ）
成立的函数是（ ）
成立的函数是（ ）