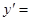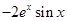题目内容
设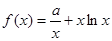 ,
,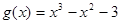
(1)当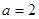 时,求曲线
时,求曲线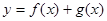 在
在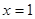 处的切线方程
处的切线方程
(2)如果对任意的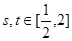 ,恒有
,恒有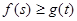 成立,求实数
成立,求实数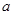 的取值范围
的取值范围
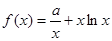 ,
,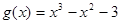
(1)当
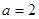 时,求曲线
时,求曲线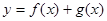 在
在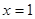 处的切线方程
处的切线方程(2)如果对任意的
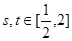 ,恒有
,恒有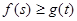 成立,求实数
成立,求实数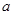 的取值范围
的取值范围(1)令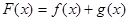 ,则
,则
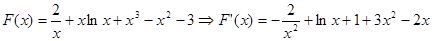
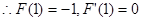
故 曲线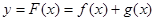 在
在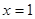 处的切线方程为
处的切线方程为 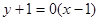 ,
,
即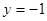 (4分)
(4分)
(2)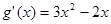 ,令
,令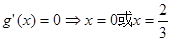
而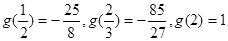 ,故
,故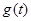 在
在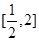 上
上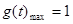 (6分)
(6分)
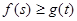 在
在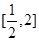 上恒成立
上恒成立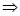
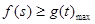 在
在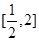 上恒成立
上恒成立
即 在
在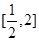 上恒成立
上恒成立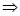
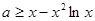 在
在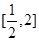 上恒成立 (7分)
上恒成立 (7分)
记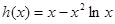
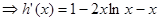 ,则
,则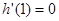 (8分)
(8分)
下证明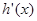 在
在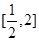 上是单调减的
上是单调减的
【 记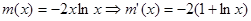 ,
,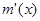 在
在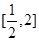 上是单调减的
上是单调减的
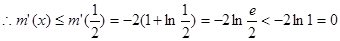
因此,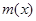 在
在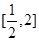 上是单调减的
上是单调减的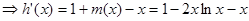
在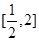 上是单调减的】 (11分)
上是单调减的】 (11分)
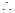
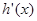 在
在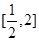 内有且只有一个零点,即为
内有且只有一个零点,即为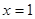
当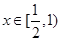 时,
时,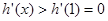
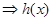 是增的
是增的
当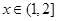 时,
时,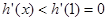
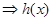 是减的
是减的
故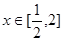 时,
时,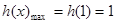
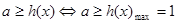 ,即
,即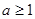
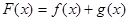 ,则
,则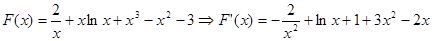
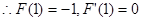
故 曲线
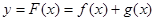 在
在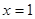 处的切线方程为
处的切线方程为 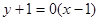 ,
,即
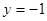 (4分)
(4分)(2)
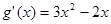 ,令
,令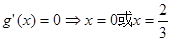
而
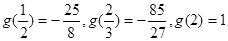 ,故
,故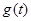 在
在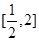 上
上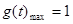 (6分)
(6分)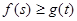 在
在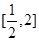 上恒成立
上恒成立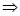
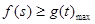 在
在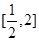 上恒成立
上恒成立 即
 在
在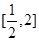 上恒成立
上恒成立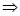
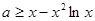 在
在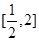 上恒成立 (7分)
上恒成立 (7分)记
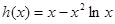
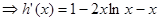 ,则
,则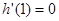 (8分)
(8分)下证明
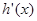 在
在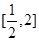 上是单调减的
上是单调减的【 记
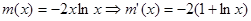 ,
,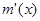 在
在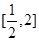 上是单调减的
上是单调减的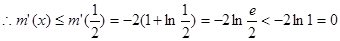
因此,
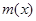 在
在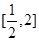 上是单调减的
上是单调减的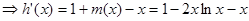
在
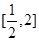 上是单调减的】 (11分)
上是单调减的】 (11分)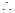
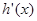 在
在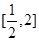 内有且只有一个零点,即为
内有且只有一个零点,即为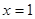
当
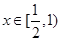 时,
时,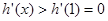
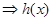 是增的
是增的当
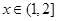 时,
时,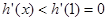
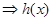 是减的
是减的故
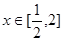 时,
时,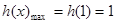
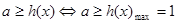 ,即
,即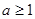
(1)求导,代入得;(2)任意的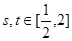 ,恒有
,恒有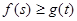 成立,得
成立,得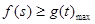
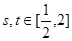 ,恒有
,恒有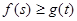 成立,得
成立,得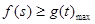

练习册系列答案
相关题目
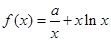 ,
, 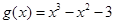 .
.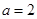 时,求曲线
时,求曲线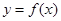 在
在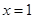 处的切线方程;
处的切线方程;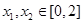 ,使得
,使得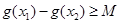 成立,求满足上述条件的最大整数
成立,求满足上述条件的最大整数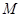 ;
;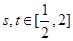 ,都有
,都有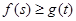 成立,求实数
成立,求实数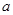 的取值范围.
的取值范围. ,
, ,
, ,则函数
,则函数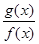 在
在 处的导数值为( )
处的导数值为( )
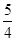

 都是定义在
都是定义在 上的函数,
上的函数,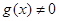 ,若
,若 ,且
,且 且
且 )及
)及 ,则
,则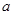 的值为 .
的值为 . 在点
在点 处切线的倾斜角的大小是 _____.
处切线的倾斜角的大小是 _____.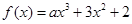 ,若
,若 ,则
,则 的值等于
的值等于
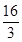

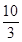
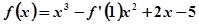 ,则
,则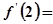 ( ▲ )
( ▲ )



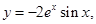 则
则