题目内容
若直线的倾斜角为α,且满足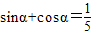 ,则直线的斜率为( )
,则直线的斜率为( )A.

B.
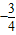
C.
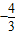
D.
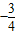 或
或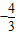
【答案】分析:由直线L的倾斜角为α,知直线的斜率k=tanα,设tan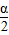 =x,则sinα=
=x,则sinα=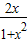 ,cosα=
,cosα=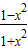 ,tanα=
,tanα=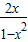 ,由此利用sinα+cosα=
,由此利用sinα+cosα= ,能求出直线的斜率.
,能求出直线的斜率.
解答:解:∵直线L的倾斜角为α,∴直线的斜率k=tanα,
设tan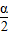 =x,则sinα=
=x,则sinα=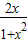 ,cosα=
,cosα=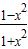 ,tanα=
,tanα=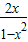 ,
,
∵α∈[0°,180°],∴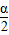 ∈[0°,90°],
∈[0°,90°],
∴tan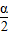 >0,x>0,
>0,x>0,
∵sinα+cosα= ,
,
∴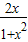 +
+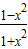 =
= ,
,
∴6x2-10x-4=0,
解得x=2,或x=- (舍去)
(舍去)
因此tanα=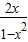 =-
=- ,
,
∴直线的斜率k=tanα=- .
.
故选C
点评:本题考查直线的斜率的求法,是基础题.解题时要认真审题,仔细解答,注意合理地进行等价转化.
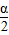 =x,则sinα=
=x,则sinα=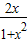 ,cosα=
,cosα=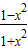 ,tanα=
,tanα=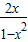 ,由此利用sinα+cosα=
,由此利用sinα+cosα= ,能求出直线的斜率.
,能求出直线的斜率.解答:解:∵直线L的倾斜角为α,∴直线的斜率k=tanα,
设tan
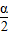 =x,则sinα=
=x,则sinα=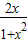 ,cosα=
,cosα=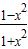 ,tanα=
,tanα=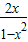 ,
,∵α∈[0°,180°],∴
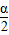 ∈[0°,90°],
∈[0°,90°],∴tan
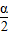 >0,x>0,
>0,x>0,∵sinα+cosα=
 ,
,∴
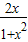 +
+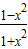 =
= ,
,∴6x2-10x-4=0,
解得x=2,或x=-
 (舍去)
(舍去)因此tanα=
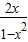 =-
=- ,
,∴直线的斜率k=tanα=-
 .
.故选C
点评:本题考查直线的斜率的求法,是基础题.解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若直线的倾斜角为120°,则直线的斜率为( )
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|