题目内容
（2011•西山区模拟）已知向量
=(1，3)，
=(-2，m)，若
与
+2
垂直，则m的值为（ ）
| a |
| b |
| a |
| a |
| b |
分析：根据向量坐标运算的公式，求出向量
+2
的坐标．再利用向量
与
+2
互相垂直，得到它们的数量积等于0，利用两个向量数量积的坐标表达式列方程，可求解m的值．
| a |
| b |
| a |
| a |
| b |
解答：解∵
=(1，3)，
=(-2，m)
∴向量
+2
=（1-4，3+2m）=（-3，3+2m）
又∵向量
与
+2
互相垂直，
∴
•（
+2
）=1×（-3）+3（3+2m）=0
∴-3+9+6m=0⇒m=-1
故选B．
| a |
| b |
∴向量
| a |
| b |
又∵向量
| a |
| a |
| b |
∴
| a |
| a |
| b |
∴-3+9+6m=0⇒m=-1
故选B．
点评：本题根据两个向量垂直，求参数m的值，考查了向量坐标的线性运算、向量数量积的坐标公式和两个向量垂直的充要条件等知识点，属于基础题．
练习册系列答案
寒假大串联黄山书社系列答案
相关题目
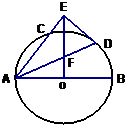（2011•西山区模拟）如图，AB是⊙O的直径，AC是弦，∠BAC的平分线AD交⊙O于D，DE⊥AC交AC延长线于点E，OE交AD于点F．