题目内容
直线l方程是x+2y+3=0,曲线C的极坐标方程是ρ2-2| 2 |
(1)分别求直线l和曲线C的参数方程;
(2)求直线l和曲线C交点的直角坐标.
分析:(1)将直线方程化成
(t为参数)这种形式即可,利用
将曲线C的极坐标方程化成普通方程,再化成参数方程即可;
(2)先将曲线C化简成普通方程,然后联立直线方程与曲线C的方程求出方程组的解,求出的解就是交点坐标.
|
|
(2)先将曲线C化简成普通方程,然后联立直线方程与曲线C的方程求出方程组的解,求出的解就是交点坐标.
解答:解:(1)直线l的参数方程为
(t为参数),(2分)
(或
(t为参数);或
(t为参数).等形式均可
曲线C的参数方程是
(θ为参数)(5分)
(2)直线l的普通方程为x+2y+3=0,
曲线C普通方程为(x-1)2+(y-1)2=9,(7分)
联立
,
解得交点的直角坐标为A(1,-2),B(-
,-
)(10分)
|
(或
|
|
曲线C的参数方程是
|
(2)直线l的普通方程为x+2y+3=0,
曲线C普通方程为(x-1)2+(y-1)2=9,(7分)
联立
|
解得交点的直角坐标为A(1,-2),B(-
| 7 |
| 5 |
| 4 |
| 5 |
点评:本题综合考查了直线的参数方程,以及圆的参数方程和极坐标方程等有关知识,属于基础题.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
 ρsin(θ+45°)-7=0.
ρsin(θ+45°)-7=0.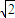 ρsin(θ+45°)-7=0.
ρsin(θ+45°)-7=0.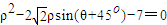 .
.