题目内容
椭圆以坐标轴为对称轴,且经过点(1,
)、(-2,0).记其上顶点为A,右顶点为B.
(1)求圆心在线段AB上,且与坐标轴相切于椭圆焦点的圆的方程;
(2)在椭圆位于第一象限的弧AB上求一点M,使△MAB的面积最大.
| 3 | 2 |
(1)求圆心在线段AB上,且与坐标轴相切于椭圆焦点的圆的方程;
(2)在椭圆位于第一象限的弧AB上求一点M,使△MAB的面积最大.
分析:(1)先求出椭圆方程、直线AB方程,再利用点到直线的距离公式,即可求出圆的方程;
(2)法一参数法;法二:设与AB平行的直线为
x+2y+p=0,当此直线与椭圆相切于第一象限时,切点即所求M点.
(2)法一参数法;法二:设与AB平行的直线为
| 3 |
解答:解:设椭圆方程为Ax2+By2=1,则
将(1,
)、(-2,0)代入有:
,
解得:
,∴椭圆方程为:
+
=1(4分)
故有A(0,
),B(2,0),右焦点(1,0)
直线AB方程为:
+
=1,即:
x+2y-2
=0(7分)
(1)由题意知圆心(a,b)在第一象限,圆与X轴相切于(1,0),故a=1
代入
x+2y-2
=0,求得:b=
,半径r=b=
故圆的方程为:(x-1)2+(y-
)2=
(或:x2+y2-2x-
y+1=0)(10分)
(2)法一:设M(2cosθ,
sinθ)(0<θ<
)
则M到直线AB距离为:d=
=
由0<θ<
知当θ=
时,|
sin(θ+
)-1|取最大值,d取最大值.
∵AB长为定值,故此时△MAB的面积最大,得M(
,
)(14分)
法二:设与AB平行的直线为
x+2y+p=0,
当此直线与椭圆相切于第一象限时,切点即所求M点.
由
得:6x2+2
px+p2-12=0①
令①中△=0,有:12×(24-p2)=0
又直线过第一象限,故p<0,解得p=-2
,
此时由①有x=-
=
代入椭圆方程,取y>0,解得y=
.故M(
,
).
将(1,
| 3 |
| 2 |
|
解得:
|
| x2 |
| 4 |
| y2 |
| 3 |
故有A(0,
| 3 |
直线AB方程为:
| x |
| 2 |
| y | ||
|
| 3 |
| 3 |
(1)由题意知圆心(a,b)在第一象限,圆与X轴相切于(1,0),故a=1
代入
| 3 |
| 3 |
| ||
| 2 |
| ||
| 2 |
故圆的方程为:(x-1)2+(y-
| ||
| 2 |
| 3 |
| 4 |
| 3 |
(2)法一:设M(2cosθ,
| 3 |
| π |
| 2 |
则M到直线AB距离为:d=
|2
| ||||||
|
2
| ||||||
|
由0<θ<
| π |
| 2 |
| π |
| 4 |
| 2 |
| π |
| 4 |
∵AB长为定值,故此时△MAB的面积最大,得M(
| 2 |
| ||
| 2 |
法二:设与AB平行的直线为
| 3 |
当此直线与椭圆相切于第一象限时,切点即所求M点.
由
|
| 3 |
令①中△=0,有:12×(24-p2)=0
又直线过第一象限,故p<0,解得p=-2
| 6 |
此时由①有x=-
2
| ||
| 2×6 |
| 2 |
代入椭圆方程,取y>0,解得y=
| ||
| 2 |
| 2 |
| ||
| 2 |
点评:本题考查直线方程、椭圆方程、圆的方程,考查直线与圆的位置关系,考查参数法的运用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
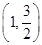 、
、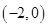 .记其上顶点为
.记其上顶点为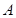 ,右顶点为
,右顶点为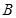 .
.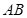 上,且与坐标轴相切于椭圆焦点的圆的方程;
上,且与坐标轴相切于椭圆焦点的圆的方程;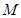 ,使
,使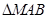 的面积最大.
的面积最大.