题目内容
(本小题满分14分)
已知A(-1,2)为抛物线C: y=2x2上的点,直线 过点A,且与抛物线C 相切,直线
过点A,且与抛物线C 相切,直线 :x=a(a≠-1)交抛物线C于B,交直线
:x=a(a≠-1)交抛物线C于B,交直线 于点D.
于点D.
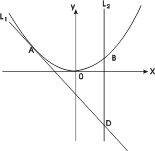
(1)求直线 的方程.
的方程.
(2)设 的面积为S1,求
的面积为S1,求 及S1的值.
及S1的值.
(3)设由抛物线C,直线 所围成的图形的面积为S2,求证S1:S2的值为与a无关的常数.
所围成的图形的面积为S2,求证S1:S2的值为与a无关的常数.
已知A(-1,2)为抛物线C: y=2x2上的点,直线
 过点A,且与抛物线C 相切,直线
过点A,且与抛物线C 相切,直线 :x=a(a≠-1)交抛物线C于B,交直线
:x=a(a≠-1)交抛物线C于B,交直线 于点D.
于点D.
(1)求直线
 的方程.
的方程.(2)设
 的面积为S1,求
的面积为S1,求 及S1的值.
及S1的值.(3)设由抛物线C,直线
 所围成的图形的面积为S2,求证S1:S2的值为与a无关的常数.
所围成的图形的面积为S2,求证S1:S2的值为与a无关的常数.(1)由 当x=1时,y'=-4 ………………2分
当x=1时,y'=-4 ………………2分
∴ 的方程为y-2=-4(x+1)即y=-4x-2 ……………………3分(2)
的方程为y-2=-4(x+1)即y=-4x-2 ……………………3分(2) 得B点坐标为(
得B点坐标为(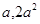 ) ……………………4分
) ……………………4分
由 得D点坐标(
得D点坐标(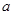 ,-4
,-4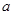 -2) ……………………5分
-2) ……………………5分
点A 到直线BD的距离为 ………………………………6分
………………………………6分
 = 2
= 2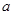 2+4
2+4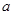 +2=2(
+2=2(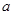 +1)2
+1)2
∴S1= ………………………………7分
………………………………7分
(3)当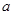 >-1时,S1=(
>-1时,S1=(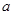 +1)3, ………………………………………8分
+1)3, ………………………………………8分

 …………………………………………9分
…………………………………………9分
…………………………………………10分
∴S1:S2= ………………………………………………………………………11分
………………………………………………………………………11分
当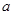 <-1时,S1= -(
<-1时,S1= -(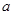 +1)3 ……………………………………………………12
+1)3 ……………………………………………………12
 ……………………………………………13分
……………………………………………13分
∴S1:S2=
综上可知S1:S2的值为与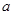 无关的常数,这常数是
无关的常数,这常数是 …………………………………14分
…………………………………14分
 当x=1时,y'=-4 ………………2分
当x=1时,y'=-4 ………………2分∴
 的方程为y-2=-4(x+1)即y=-4x-2 ……………………3分(2)
的方程为y-2=-4(x+1)即y=-4x-2 ……………………3分(2) 得B点坐标为(
得B点坐标为(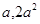 ) ……………………4分
) ……………………4分由
 得D点坐标(
得D点坐标(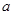 ,-4
,-4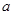 -2) ……………………5分
-2) ……………………5分点A 到直线BD的距离为
 ………………………………6分
………………………………6分 = 2
= 2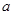 2+4
2+4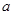 +2=2(
+2=2(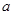 +1)2
+1)2∴S1=
 ………………………………7分
………………………………7分(3)当
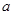 >-1时,S1=(
>-1时,S1=(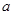 +1)3, ………………………………………8分
+1)3, ………………………………………8分
 …………………………………………9分
…………………………………………9分…………………………………………10分
∴S1:S2=
 ………………………………………………………………………11分
………………………………………………………………………11分当
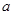 <-1时,S1= -(
<-1时,S1= -(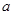 +1)3 ……………………………………………………12
+1)3 ……………………………………………………12 ……………………………………………13分
……………………………………………13分∴S1:S2=

综上可知S1:S2的值为与
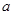 无关的常数,这常数是
无关的常数,这常数是 …………………………………14分
…………………………………14分略

练习册系列答案
相关题目
 若
若 则
则 展开式中常数项为 。
展开式中常数项为 。
 与直线
与直线 所围成的封闭图形的面积为( )
所围成的封闭图形的面积为( )



 ,当自变量x由
,当自变量x由 增加到
增加到 时,函数值的改变量是( )
时,函数值的改变量是( )



 的值为 。
的值为 。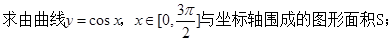 (要求画出简图解答)
(要求画出简图解答)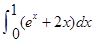 等于( )
等于( )


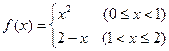 则
则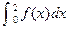 =
=