题目内容
函数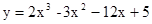 在
在 上的最大值和最小值分别是
上的最大值和最小值分别是
| A.5,-15 | B.5, -4 | C.-4,-15 | D.5,-16 |
A
解析试题分析:由题设知y'=6x2-6x-12,令y'>0,解得x>2,或x<-1,
故函数y=2x3-3x2-12x+5在[0,2]上减,在[2,3]上增,
当x=0,y=5;当x=3,y=-4;当x=2,y=-15.
由此得函数y=2x3-3x2-12x+5在[0,3]上的最大值和最小值分别是5,-15;
故答案为 A
考点:本试题主要考查了导数在研究函数中的运用,求解函数的最值。
点评:解决该试题的关键是对函数求导,利用导数求研究函数y=2x3-3x2-12x+5在[0,3]上的单调性,判断出最大值与最小值位置。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
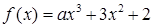 ,若
,若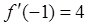 ,则
,则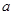 的值等于( )
的值等于( )
A.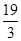 | B.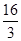 | C.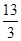 | D.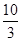 |
曲线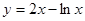 在点
在点 处的切线方程为
处的切线方程为
A.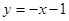 | B. |
C.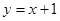 | D.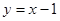 |
设函数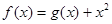 ,曲线
,曲线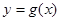 在点
在点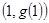 处的切线方程为
处的切线方程为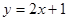 ,则曲线
,则曲线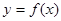 在点
在点 处的切线的斜率为( )
处的切线的斜率为( )
A.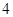 | B.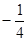 | C. | D.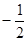 |
已知函数y=x -3x+c的图像与x轴恰有两个公共点,则c= ( )
-3x+c的图像与x轴恰有两个公共点,则c= ( )
| A.-2或2 | B.-9或3 | C.-1或1 | D.-3或1 |
曲线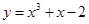 在点
在点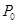 处的切线平行于直线
处的切线平行于直线 ,则点
,则点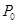 的坐标可为( )
的坐标可为( )
| A.(0,1) | B.(1,0) | C.(-1,0) | D.(1,4) |
曲线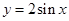 在点
在点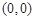 处的切线与直线
处的切线与直线 垂直,则实数
垂直,则实数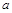 的值为( )
的值为( )
| A.2 | B.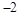 | C.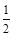 | D.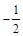 |
已知曲线 的一条切线的斜率为
的一条切线的斜率为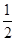 ,则切点的横坐标为( )
,则切点的横坐标为( )
| A.3 | B.2 | C.1 | D.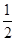 |
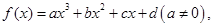 记
记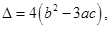 则当
则当 的大致图像为( )
的大致图像为( )