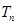题目内容
.(本小题14分)
已知函数 ,其中
,其中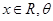 为参数,且
为参数,且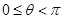 .
.
(1)当 时,判断函数
时,判断函数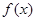 是否有极值,说明理由;
是否有极值,说明理由;
(2)要使函数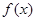 的极小值大于零,求参数
的极小值大于零,求参数 的取值范围;
的取值范围;
(3)若对(2)中所求的取值范围内的任意参数 ,函数
,函数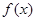 在区间
在区间 内都是增函数,求实数
内都是增函数,求实数 的取值范围。
的取值范围。
【答案】
解:(1)当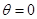 即
即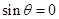 时
时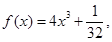 则
则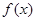 在
在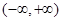 内是增函数,故无极值。…………3分
内是增函数,故无极值。…………3分
(2)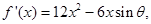 令
令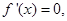 得
得
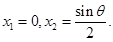
由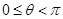 及(1),只需考虑
及(1),只需考虑 的情况。
…………5分
的情况。
…………5分
当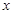 变化时,
变化时, 的符号及
的符号及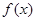 的变化情况如下表:
的变化情况如下表:
|
|
|
0 |
|
|
|
|
|
+ |
0 |
- |
0 |
+ |
|
|
增 |
极大值 |
减 |
极小值 |
增 |
因此,函数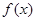 在
在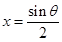 处取得极小值
处取得极小值 且
且
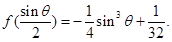
要使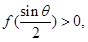 必有
必有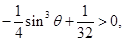 可得
可得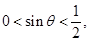 所以
所以
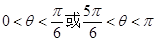 …………9分
…………9分
(3)解:由(2)知,函数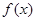 在区间
在区间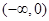 与
与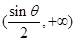 内都是增函数。
内都是增函数。
由题设,函数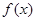 在
在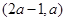 内是增函数,则
内是增函数,则 须满足不等式组
须满足不等式组
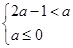 或
或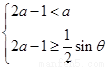 13分
13分
由(2)中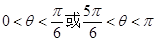 时,
时,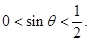 要使不等式
要使不等式 关于参数
关于参数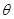 恒成立,必有
恒成立,必有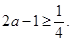
综上所述,  的取值范围是
的取值范围是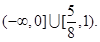 …………14分
…………14分
【解析】略

练习册系列答案
相关题目


 (本小题14分)右图是一个直三棱柱(以
(本小题14分)右图是一个直三棱柱(以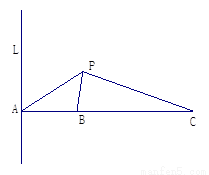
 km,用
km,用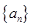 中,
中,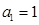 ,前
,前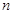 项和
项和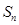 满足条件
满足条件 ,
,
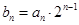 ,求数列
,求数列 的前
的前