题目内容
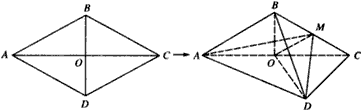
 如图,已知菱形ABCD的边长为2,∠BAD=60°,S为平面ABCD外一点,△SAD为正三角形,SB=
如图,已知菱形ABCD的边长为2,∠BAD=60°,S为平面ABCD外一点,△SAD为正三角形,SB=| 6 |
(Ⅰ)求证:平面SAD⊥平面ABCD;
(Ⅱ)求二面角A-SB-C的余弦值;
(Ⅲ)求四棱锥M-ABN的体积.
分析:(Ⅰ)证明平面SAD⊥平面ABCD,我们只要在一个平面内找出另一平面的垂线,取AD的中点O,连接SO,BO,即证SO⊥平面ABCD,从而只需证SO垂直于平面内的两条相交直线;
(Ⅱ)先证明AM⊥SB,MN⊥SB,所以∠AMN为二面角A-SB-C的平面角,再由OM⊥平面SBC,可得∠OMN=90°,从而可得sin∠AMO=
=
,进而可求二面角A-SB-C的余弦值;
(Ⅲ)先求出S△BMN=
,根据OM⊥平面SBC,可得O点到平面BNM的距离,再利用AO∥平面SBC,可得A点到平面BNM的距离等于O点到平面BNM的距离,从而可求三棱锥M-ABN的体积.
(Ⅱ)先证明AM⊥SB,MN⊥SB,所以∠AMN为二面角A-SB-C的平面角,再由OM⊥平面SBC,可得∠OMN=90°,从而可得sin∠AMO=
| AO |
| AM |
| ||
| 5 |
(Ⅲ)先求出S△BMN=
| ||
| 4 |
解答: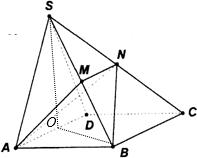 (Ⅰ)证明:取AD的中点O,连接SO,BO
(Ⅰ)证明:取AD的中点O,连接SO,BO
因为△SAD为正三角形,所以SO⊥AD,且SO=
又菱形ABCD的边长为2,∠BAD=60°,所以BO=
而SB=
,所以SB2=SO2+BO2,即SO⊥BO
因为BO∩AD=O
所以SO⊥平面ABCD,又SO⊆平面SAD
所以平面SAD⊥平面ABCD;
(Ⅱ)解:因为SA=AB=2,点M为SB的中点,所以AM⊥SB
由(Ⅰ)知BC⊥SO,又菱形ABCD的边长为2,∠BAD=60°,所以BC⊥BO
因为SO∩BO=O
所以BC⊥面SOB
因为SB⊆面SOB
所以BC⊥SB
因为点N为SC的中点,所以MN∥BC,故MN⊥SB
所以∠AMN为二面角A-SB-C的平面角
又平面SOB⊥平面SBC,连接OM,则OM⊥SB,
所以OM⊥平面SBC
所以∠OMN=90°
在直角三角形AOM中,AO=1,MO=
,所以AM=
,
所以sin∠AMO=
=
∴cos∠AMN=cos(90°+∠AMO)=-sin∠AMO=-
∴二面角A-SB-C的余弦值-
;
(Ⅲ)解:由(Ⅱ)知,MN⊥SB,因为MN=
BC=1,MB=
,
所以S△BMN=
又OM⊥平面SBC,所以O点到平面BNM的距离为MO=
因为AO∥BC,AO?平面SBC,所以AO∥平面SBC
所以A点到平面BNM的距离等于O点到平面BNM的距离MO=
所以三棱锥M-ABN的体积为
×S△BMN×OM=
×
×
=
 (Ⅰ)证明:取AD的中点O,连接SO,BO
(Ⅰ)证明:取AD的中点O,连接SO,BO因为△SAD为正三角形,所以SO⊥AD,且SO=
| 3 |
又菱形ABCD的边长为2,∠BAD=60°,所以BO=
| 3 |
而SB=
| 6 |
因为BO∩AD=O
所以SO⊥平面ABCD,又SO⊆平面SAD
所以平面SAD⊥平面ABCD;
(Ⅱ)解:因为SA=AB=2,点M为SB的中点,所以AM⊥SB
由(Ⅰ)知BC⊥SO,又菱形ABCD的边长为2,∠BAD=60°,所以BC⊥BO
因为SO∩BO=O
所以BC⊥面SOB
因为SB⊆面SOB
所以BC⊥SB
因为点N为SC的中点,所以MN∥BC,故MN⊥SB
所以∠AMN为二面角A-SB-C的平面角
又平面SOB⊥平面SBC,连接OM,则OM⊥SB,
所以OM⊥平面SBC
所以∠OMN=90°
在直角三角形AOM中,AO=1,MO=
| ||
| 2 |
| ||
| 2 |
所以sin∠AMO=
| AO |
| AM |
| ||
| 5 |
∴cos∠AMN=cos(90°+∠AMO)=-sin∠AMO=-
| ||
| 5 |
∴二面角A-SB-C的余弦值-
| ||
| 5 |
(Ⅲ)解:由(Ⅱ)知,MN⊥SB,因为MN=
| 1 |
| 2 |
| ||
| 2 |
所以S△BMN=
| ||
| 4 |
又OM⊥平面SBC,所以O点到平面BNM的距离为MO=
| ||
| 2 |
因为AO∥BC,AO?平面SBC,所以AO∥平面SBC
所以A点到平面BNM的距离等于O点到平面BNM的距离MO=
| ||
| 2 |
所以三棱锥M-ABN的体积为
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 4 |
| ||
| 2 |
| 1 |
| 4 |
点评:本题以四棱锥为载体,考查面面垂直的判定,考查面面角,考查三棱锥的体积,解题的关键是正确运用面面垂直的判定定理,寻找面面角,同时考查学生转化问题的能力.

练习册系列答案
相关题目
 (2012•邯郸一模)如图,已知四棱锥E-ABCD的底面为菱形,且∠ABC=60°,AB=EC=2,AE=BE=
(2012•邯郸一模)如图,已知四棱锥E-ABCD的底面为菱形,且∠ABC=60°,AB=EC=2,AE=BE= 如图,已知在四棱锥P-ABCD中,底面ABCD是菱形,PA⊥底面ABCD,AB=1,PA•AC=1,∠ABC=θ(0<θ<
如图,已知在四棱锥P-ABCD中,底面ABCD是菱形,PA⊥底面ABCD,AB=1,PA•AC=1,∠ABC=θ(0<θ<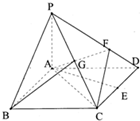 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,点E、G分别是CD、PC的中点,点F在PD上,且PF:FD=2:1.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,点E、G分别是CD、PC的中点,点F在PD上,且PF:FD=2:1. 。
。