题目内容
(本小题满分12分)
已知f(x)=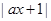 (a∈R),不等式f(x)≤3的解集为{x|?2≤x≤1}.
(a∈R),不等式f(x)≤3的解集为{x|?2≤x≤1}.
(Ⅰ)求a的值;
(Ⅱ)若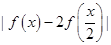 ≤k恒成立,求k的取值范围.
≤k恒成立,求k的取值范围.
(Ⅰ)a =2.(Ⅱ)k≥1.
解析试题分析:(I)本小题属于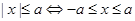 这种类型的不等式.
这种类型的不等式.
(II)先根据h(x)= f(x)?2f ,得 h(x)=
,得 h(x)= ,
,
从而可得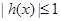 ,因而
,因而 .
.
(Ⅰ) 由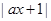 ≤3得?4≤ax≤2, f(x)≤3的解集为{x|?2≤x≤1},
≤3得?4≤ax≤2, f(x)≤3的解集为{x|?2≤x≤1},
当a≤0时,不合题意.
当a>0时,?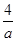 ≤x≤
≤x≤ 得a =2.……………………………………5分
得a =2.……………………………………5分
(Ⅱ)记h(x)= f(x)?2f ,则 h(x)=
,则 h(x)=
所以|h(x)|≤1,因此k≥1.
考点:本小题考查了绝对值不等式,分段函数的值域,及不等式恒成立问题.
点评:掌握常见不等式类型的解法是求解此类问题的关键,对于绝对值不等式一般有两种类型:(1)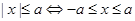 .(2)
.(2) 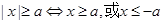 .
.

练习册系列答案
相关题目
下列命题中正确的是
A.当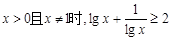 |
B.当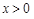 , ,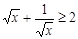 |
C.当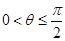 , ,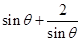 的最小值为 的最小值为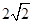 |
D.当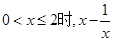 无最大值 无最大值 |
已知a>0,b>0,若不等式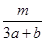 -
-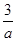 -
-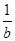 ≤0恒成立,则m的最大值为( )
≤0恒成立,则m的最大值为( )
| A.4 | B.16 | C.9 | D.3 |
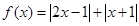 .
.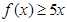 ;
;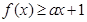 的解集为
的解集为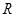 ,求实数
,求实数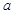 的取值范围.
的取值范围.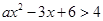 的解集为
的解集为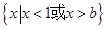 .
.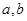 ;
;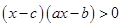 .
.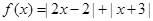 .
.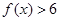 ;
; 的不等式
的不等式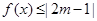 的解集不是空集,试求实数
的解集不是空集,试求实数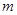 的取值范围.
的取值范围. 的不等式
的不等式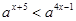 (
(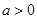 ,且
,且 ).
).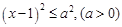 的解集为A,函数
的解集为A,函数 的定义域为B.
的定义域为B.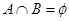 ,求
,求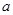 的取值范围;
的取值范围; 的图象关于原点对称。
的图象关于原点对称。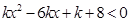 的解集为空集,求实数k的取值范围.
的解集为空集,求实数k的取值范围.