题目内容
已知函数y=
+（m2-mx+1）的定义域为R，则m的取值范围是（ ）A．（
-1，2）B．（
-1，+∞）C．（-2，2）
D．（-1-
，-1
）
【答案】分析：变原函数中的分数指数幂为根式，然后求使分母中根式内部的代数式恒大于0的x的取值范围．
解答：解：原函数化为
，
因为原函数的定义域为R，所以对任意x∈R，mx2+4x+m+2＞0恒成立，
当m=0时不合题意，
所以有
，解得：m＞
所以m的取值范围是（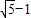
，+∞）．
故选B．
点评：本题考查了函数定义域的求法，考查了分类讨论的数学思想，是易错题．
解答：解：原函数化为
，因为原函数的定义域为R，所以对任意x∈R，mx2+4x+m+2＞0恒成立，
当m=0时不合题意，
所以有
，解得：m＞所以m的取值范围是（
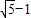，+∞）．故选B．
点评：本题考查了函数定义域的求法，考查了分类讨论的数学思想，是易错题．
练习册系列答案
相关题目