题目内容
已知函数 ,且
,且 是函数
是函数 的一个极小值点.
的一个极小值点.
(Ⅰ)求实数 的值;
的值;
(Ⅱ)求 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.
(Ⅰ)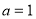 ;(Ⅱ)当
;(Ⅱ)当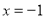 或
或 时,
时,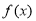 有最小值
有最小值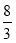 ;当
;当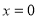 或
或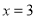 时,
时,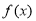 有最大值
有最大值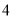 .
.
【解析】
试题分析:(Ⅰ)先求函数的导函数,因为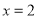 是函数
是函数 的一个极小值点,所以
的一个极小值点,所以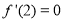 ,即可求得
,即可求得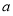 的值。(Ⅱ)由(Ⅰ)知,
的值。(Ⅱ)由(Ⅰ)知,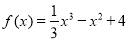 ,求导,在令导数等于0,讨论导数的正负可得函数的单调区间,根据函数的单调区间可求其最值。
,求导,在令导数等于0,讨论导数的正负可得函数的单调区间,根据函数的单调区间可求其最值。
试题解析:【解析】
(Ⅰ)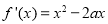 . 2分
. 2分
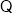
 是函数
是函数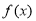 的一个极小值点,
的一个极小值点,

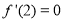 .
.
即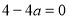 ,解得
,解得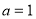 . 4分
. 4分
经检验,当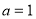 时,
时, 是函数
是函数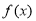 的一个极小值点.
的一个极小值点.
 实数
实数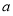 的值为
的值为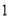 . 5分
. 5分
(Ⅱ)由(Ⅰ)知,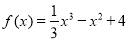 .
.
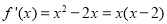 .
.
令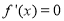 ,得
,得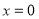 或
或 . 6分
. 6分
当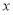 在
在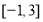 上变化时,
上变化时,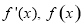 的变化情况如下:
的变化情况如下:
 9分
9分
当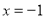 或
或 时,
时,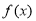 有最小值
有最小值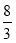
当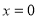 或
或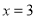 时,
时,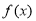 有最大值
有最大值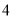 . 11分
. 11分
考点:1求导数;2用导数研究函数的单调性。

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目