题目内容
设集合A={(x,y)|y=2x-1,x∈N*},B={(x,y)|y=ax2-ax+a,x∈N*},问是否存在非零整数a,使A∩B≠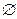 ?若存在,请求出a的值;若不存在,说明理由.
?若存在,请求出a的值;若不存在,说明理由.
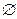 ?若存在,请求出a的值;若不存在,说明理由.
?若存在,请求出a的值;若不存在,说明理由.存在a=1,使得A∩B≠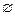 ,此时A∩B={(1,1),(2,3)}.
,此时A∩B={(1,1),(2,3)}.
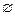 ,此时A∩B={(1,1),(2,3)}.
,此时A∩B={(1,1),(2,3)}.假设A∩B≠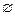 ,则方程组
,则方程组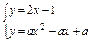 有正整数解,消去y,
有正整数解,消去y,
得ax2-(a+2)x+a+1="0. " (*)
由Δ≥0,有(a+2)2-4a(a+1)≥0,解得-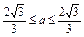 .因a为非零整数,∴a=±1,
.因a为非零整数,∴a=±1,
当a=-1时,代入(*),解得x=0或x=-1,而x∈N*.故a≠-1.当a=1时,代入(*),
解得x=1或x=2,符合题意.故存在a=1,使得A∩B≠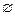 ,此时A∩B={(1,1),(2,3)}.
,此时A∩B={(1,1),(2,3)}.
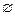 ,则方程组
,则方程组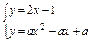 有正整数解,消去y,
有正整数解,消去y,得ax2-(a+2)x+a+1="0. " (*)
由Δ≥0,有(a+2)2-4a(a+1)≥0,解得-
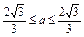 .因a为非零整数,∴a=±1,
.因a为非零整数,∴a=±1,当a=-1时,代入(*),解得x=0或x=-1,而x∈N*.故a≠-1.当a=1时,代入(*),
解得x=1或x=2,符合题意.故存在a=1,使得A∩B≠
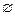 ,此时A∩B={(1,1),(2,3)}.
,此时A∩B={(1,1),(2,3)}.
练习册系列答案
相关题目
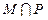 中的元素的个数为 ( )
中的元素的个数为 ( )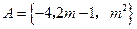 ,
,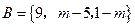 ,又
,又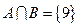 ,求实数
,求实数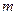 .
.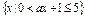 ,集合B=
,集合B=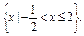
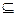 B,求实数a的取值范围;
B,求实数a的取值范围;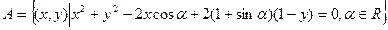 ,
, 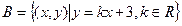 。若
。若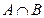 为单元素集,则
为单元素集,则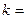 。
。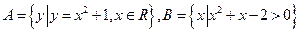 ,则下列正确的是( )
,则下列正确的是( )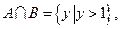



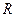 上定义运算
上定义运算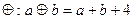 ,并定义:若
,并定义:若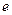 使得对
使得对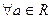 ,有
,有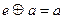 ,则
,则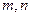 均为非负整数的有序数对
均为非负整数的有序数对 ,在做
,在做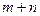 的加法运算时各位均不进位,则称
的加法运算时各位均不进位,则称