题目内容
给出下列命题:①x2≠y2?x≠y或x≠-y;
②命题“若a,b是偶数,则a+b是偶数”的逆否命题是“若a+b不是偶数,则a、b都不是偶数”;
③若“p或q”为假命题,则“非p且非q”是真命题;
④已知a、b、c是实数,关于x的不等式ax2+bx+c≤0的解集是空集,必有a>0且△≤0;
⑤设
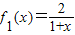 ,fn+1(x)=f1[fn(x)],且
,fn+1(x)=f1[fn(x)],且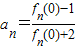 ,则a2010=
,则a2010=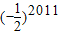 .
.正确的是 .(填番号)
【答案】分析:①x2≠y2可得x≠y且x≠-y;可判断①
②根据逆否命题是对原命题的题设和结论分别进行否定且交换题设与结论的位置可判断②
③由p或q为假命题,可知p,q都为假命题,根据复合命题的真假关系可判断③
④例如,a=b=0,c=1,关于x的不等式ax2+bx+c≤0的解集是空集,可判断④
⑤由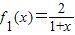 ,可得f1(0),根据已知可得an+1=
,可得f1(0),根据已知可得an+1=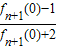 =
=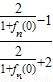
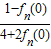 ,结合等比数列的通项公式可求an,进而可求
,结合等比数列的通项公式可求an,进而可求
解答:解;:①x2≠y2?x≠y且x≠-y;故①错误
②命题“若a,b是偶数,则a+b是偶数”的逆否命题是“若a+b不是偶数,则a、b不都是偶数”;故②错误
③若“p或q”为假命题,则p,q都为假命题,¬p,¬q都为真命题,“非p且非q”是真命题;故③正确
④例如,a=b=0,c=1,关于x的不等式ax2+bx+c≤0的解集是空集,故④错误
⑤由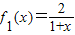 ,可得f1(0)=2
,可得f1(0)=2
∴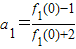 =
=
∴fn+1(0)=f1[fn(0)]=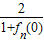
∴an+1=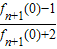 =
=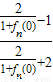
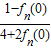 =
=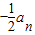
∴数列{an}是首项为 为首项,以-
为首项,以- 为公比的等比数列
为公比的等比数列
∴an=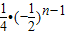
∴a =
=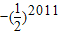 ,故 ⑤正确
,故 ⑤正确
故答案为:③⑤
点评:本题主要考查了命题的否命题的写法,复合命题的真假关系的应用及不等式的恒成立问题的应用,而⑤中的等比关系的确定是解答的难点所在.
②根据逆否命题是对原命题的题设和结论分别进行否定且交换题设与结论的位置可判断②
③由p或q为假命题,可知p,q都为假命题,根据复合命题的真假关系可判断③
④例如,a=b=0,c=1,关于x的不等式ax2+bx+c≤0的解集是空集,可判断④
⑤由
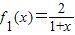 ,可得f1(0),根据已知可得an+1=
,可得f1(0),根据已知可得an+1=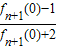 =
=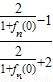
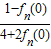 ,结合等比数列的通项公式可求an,进而可求
,结合等比数列的通项公式可求an,进而可求解答:解;:①x2≠y2?x≠y且x≠-y;故①错误
②命题“若a,b是偶数,则a+b是偶数”的逆否命题是“若a+b不是偶数,则a、b不都是偶数”;故②错误
③若“p或q”为假命题,则p,q都为假命题,¬p,¬q都为真命题,“非p且非q”是真命题;故③正确
④例如,a=b=0,c=1,关于x的不等式ax2+bx+c≤0的解集是空集,故④错误
⑤由
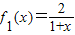 ,可得f1(0)=2
,可得f1(0)=2∴
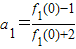 =
=
∴fn+1(0)=f1[fn(0)]=
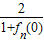
∴an+1=
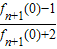 =
=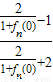
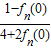 =
=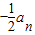
∴数列{an}是首项为
 为首项,以-
为首项,以- 为公比的等比数列
为公比的等比数列∴an=
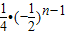
∴a
 =
=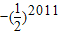 ,故 ⑤正确
,故 ⑤正确故答案为:③⑤
点评:本题主要考查了命题的否命题的写法,复合命题的真假关系的应用及不等式的恒成立问题的应用,而⑤中的等比关系的确定是解答的难点所在.

练习册系列答案
相关题目