题目内容
已知向量 ,
, ,其中ω为常数,且ω>0.
,其中ω为常数,且ω>0.(1)若ω=1,且
 ∥
∥ ,求tanx的值;
,求tanx的值;(2)设函数
 ,若f(x)的最小正周期为π,求f(x)在
,若f(x)的最小正周期为π,求f(x)在 时的值域.
时的值域.
【答案】分析:(1)由 ∥
∥ 的充要条件知,
的充要条件知, ,即
,即 ,
, ,解出x,使用周期性及诱导公式求得tanx的值.
,解出x,使用周期性及诱导公式求得tanx的值.
(2)使用二倍角公式化简f(x)的解析式,求出角的范围,再利用函数的单调性求函数的值域.
解答:解:(1)若ω=1,则 ,
, ,
,
由 ∥
∥ 的充要条件知,存在非零实数λ,使得
的充要条件知,存在非零实数λ,使得 ,即
,即 ,
,
所以, ,
, ,
,
∴ ,k∈Z,
,k∈Z, ,k∈Z,
,k∈Z, .
.
(2) =
= ,
,
因为f(x)的最小正周期为π,所以 ,ω=1,
,ω=1,
所以 ,(10分)
,(10分)
当 时,
时, ,
,
所以函数f(x)的值域为 .
.
点评:本题考查两个向量共线的性质,函数周期性的应用及诱导公式的应用,已知三角函数的值求角的大小即利用函数的单调性求函数的值域.
 ∥
∥ 的充要条件知,
的充要条件知, ,即
,即 ,
, ,解出x,使用周期性及诱导公式求得tanx的值.
,解出x,使用周期性及诱导公式求得tanx的值.(2)使用二倍角公式化简f(x)的解析式,求出角的范围,再利用函数的单调性求函数的值域.
解答:解:(1)若ω=1,则
 ,
, ,
,由
 ∥
∥ 的充要条件知,存在非零实数λ,使得
的充要条件知,存在非零实数λ,使得 ,即
,即 ,
,所以,
 ,
, ,
,∴
 ,k∈Z,
,k∈Z, ,k∈Z,
,k∈Z, .
.(2)
 =
= ,
,因为f(x)的最小正周期为π,所以
 ,ω=1,
,ω=1,所以
 ,(10分)
,(10分)当
 时,
时, ,
,所以函数f(x)的值域为
 .
.点评:本题考查两个向量共线的性质,函数周期性的应用及诱导公式的应用,已知三角函数的值求角的大小即利用函数的单调性求函数的值域.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
 ,
, ,其中
,其中 、
、 为互相垂直的单位向量,若
为互相垂直的单位向量,若 ,则tan2α的值为( )
,则tan2α的值为( )

 ,
, ,其中O为坐标原点,若|
,其中O为坐标原点,若| |≥2|
|≥2| |对任意的实数α,β都成立,则实数λ的取值范围是 .
|对任意的实数α,β都成立,则实数λ的取值范围是 . ,
, ,其中O为坐标原点,若|
,其中O为坐标原点,若|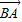 |≥2|
|≥2| |对任意的实数α,β都成立,则实数λ的取值范围是 .
|对任意的实数α,β都成立,则实数λ的取值范围是 . ,
, ,其中O为坐标原点,若|
,其中O为坐标原点,若| |≥2|
|≥2| |对任意的实数α,β都成立,则实数λ的取值范围是 .
|对任意的实数α,β都成立,则实数λ的取值范围是 . ,
,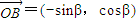 .其中O为坐标原点.
.其中O为坐标原点. 且m>0,求向量
且m>0,求向量 与
与 的夹角;
的夹角; 对任意实数α、β都成立,求实数m的取值范围.
对任意实数α、β都成立,求实数m的取值范围.