��Ŀ����
��֪����f(x)=�Rx-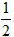 ax2+bx(a>0)�ҵ���f�F(x)=0.
ax2+bx(a>0)�ҵ���f�F(x)=0.
��1�����ú���a��ʽ�ӱ�ʾb������f(x)�ĵ������䣻
��2�����ں���ͼ���ϲ�ͬ������A(x1,y1)����x1<x2������ں���ͼ���ϴ��ڵ�M(x0,y0)������x0��(x1,x2)��ʹ�õ�M��������l//AB�����AB���ڡ��������ߡ�.�ر�أ���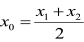 ʱ���ֳ�AB���ڡ���ֵ�������ߡ�.���ʣ��ں���f(x)���Ƿ��������A,Bʹ�������ڡ���ֵ�������ߡ��������ڣ���A,B�����꣬�������ڣ���˵������.
ʱ���ֳ�AB���ڡ���ֵ�������ߡ�.���ʣ��ں���f(x)���Ƿ��������A,Bʹ�������ڡ���ֵ�������ߡ��������ڣ���A,B�����꣬�������ڣ���˵������.
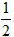 ax2+bx(a>0)�ҵ���f�F(x)=0.
ax2+bx(a>0)�ҵ���f�F(x)=0.��1�����ú���a��ʽ�ӱ�ʾb������f(x)�ĵ������䣻
��2�����ں���ͼ���ϲ�ͬ������A(x1,y1)����x1<x2������ں���ͼ���ϴ��ڵ�M(x0,y0)������x0��(x1,x2)��ʹ�õ�M��������l//AB�����AB���ڡ��������ߡ�.�ر�أ���
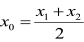 ʱ���ֳ�AB���ڡ���ֵ�������ߡ�.���ʣ��ں���f(x)���Ƿ��������A,Bʹ�������ڡ���ֵ�������ߡ��������ڣ���A,B�����꣬�������ڣ���˵������.
ʱ���ֳ�AB���ڡ���ֵ�������ߡ�.���ʣ��ں���f(x)���Ƿ��������A,Bʹ�������ڡ���ֵ�������ߡ��������ڣ���A,B�����꣬�������ڣ���˵������.�⣺
��1��f�F(x)=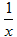 -ax+b��f�F(x)=0����b=a-1��
-ax+b��f�F(x)=0����b=a-1��
f�F(x)= =0 ��x1=-
=0 ��x1=-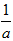 ����ȥ����x2=1��
����ȥ����x2=1��
�ຯ��f(x)�ĵ�����������Ϊ(0,1)�������ݼ�����Ϊ(1,+��)��
��2�� ������ڵ�M��������,��f�F(x0)=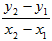 ,������:
,������: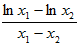 =
=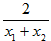 ,
,
��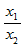 =t��(0,1),������ת��Ϊ����:�Rt=
=t��(0,1),������ת��Ϊ����:�Rt=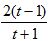 �и�,
�и�,
��g(t)=�Rt- ,g�F(t)=
,g�F(t)=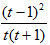 >0,
>0,
�ຯ��g(t)Ϊ(0,1)�ϵĵ�����������,��g(1)=�R1-0=0,��g(t)<0,
���Բ�����tʹ�����Rt=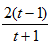 ����,�������ڵ��������⡣
����,�������ڵ��������⡣
��1��f�F(x)=
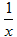 -ax+b��f�F(x)=0����b=a-1��
-ax+b��f�F(x)=0����b=a-1��f�F(x)=
 =0 ��x1=-
=0 ��x1=-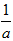 ����ȥ����x2=1��
����ȥ����x2=1�� �ຯ��f(x)�ĵ�����������Ϊ(0,1)�������ݼ�����Ϊ(1,+��)��
��2�� ������ڵ�M��������,��f�F(x0)=
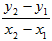 ,������:
,������: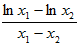 =
=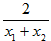 ,
, ��
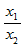 =t��(0,1),������ת��Ϊ����:�Rt=
=t��(0,1),������ת��Ϊ����:�Rt=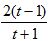 �и�,
�и�, ��g(t)=�Rt-
 ,g�F(t)=
,g�F(t)=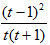 >0,
>0,�ຯ��g(t)Ϊ(0,1)�ϵĵ�����������,��g(1)=�R1-0=0,��g(t)<0,
���Բ�����tʹ�����Rt=
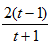 ����,�������ڵ��������⡣
����,�������ڵ��������⡣
��ϰ��ϵ�д�
 һ����ʦ�����Ծ�ϵ�д�
һ����ʦ�����Ծ�ϵ�д�
�����Ŀ
 ��֪����f(x)=
��֪����f(x)=
|
A��(
| ||||
B����
| ||||
C����
| ||||
D��[
|