题目内容
已知m、 是直线,a、β是平面,给出下列命题:
是直线,a、β是平面,给出下列命题:
(1)若l垂直于α内两条相交直线,则l⊥α;
(2)若l平行于α,则l平行于α内的所有直线;
(3)若m α,l
α,l β,且l⊥m,则α⊥β;
β,且l⊥m,则α⊥β;
(4)若l β,且l⊥α,则α⊥β;
β,且l⊥α,则α⊥β;
(5)若m α,l
α,l β,且α∥β,则l∥m.
β,且α∥β,则l∥m.
其中正确的命题的序号是________.
【答案】
(1)、(4)
【解析】
试题分析: (1)是线面垂直的判定定理,所以正确;命题(2),l∥α,但l不能平行于α内所有直线,错误;命题(3),l⊥m,不能保证l⊥α,即分别包含l与m的平面α、β可能平行也可能相交而不垂直;命题(4),为面面垂直的判定定理,所以正确;命题(5),α∥β,但分别在α、β内的直线l与m可能平行,也可能异面.
考点:线与线、线与面、面与面的位置关系;线面垂直的判定定理;线面平行的性质定理;面面垂直的判定定理;面面平行的性质定理。
点评:我们要熟练掌握线与线、线与面、面与面的位置关系以及各种判定定理和性质定理。

练习册系列答案
相关题目
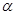 ,
,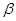 ,
,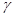 是三个两两不重合的平面,给出下列四个命题:
是三个两两不重合的平面,给出下列四个命题: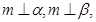 则
则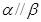 ;
; 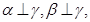 则
则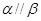 ;
;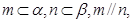 则
则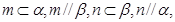 则
则