题目内容
19、在△ABC中,“cosA+sinA=cosB+sinB”是“C=90°”的( )
分析:对两个条件,“cosA+sinA=cosB+sinB”与“C=90°”的关系,拼命结合三角函数的定义,对选项进行判断
解答:解:“C=90°”成立时,有A+B=90°,故一定有“cosA+sinA=cosB+sinB”成立
又当A=B时cosA+sinA=cosB+sinB”成立,即“cosA+sinA=cosB+sinB”得不出“C=90°”成立
所以“cosA+sinA=cosB+sinB”是“C=90°”的必要百充分条件
故选B.
又当A=B时cosA+sinA=cosB+sinB”成立,即“cosA+sinA=cosB+sinB”得不出“C=90°”成立
所以“cosA+sinA=cosB+sinB”是“C=90°”的必要百充分条件
故选B.
点评:本题考查充要条件,解答本题要熟练理解掌握三角函数的定义,充分条件,必要条件的定义,且能灵活运用列举法的技巧对两个命题的关系进行验证,本题考查了推理论证的能力,解题时灵活选择证明问题的方法是解题成功的保证.

练习册系列答案
相关题目
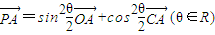 ,则
,则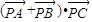 的最小值是 .
的最小值是 .