题目内容

已知三点A、B、C的坐标分别为A(cosα，sinα)(α≠
kπ
4
，k∈Z)，B（3，0），C（0，3），若
AB
•
AC
=-1，求
1+sin2α-cos2α
1+tanα
的值．
AB
=(3-cosα，-sinα)，
AC
=(-cosα，3-sinα）
∵
AC
•
BC
=-1，∴（cosα-3）•cosα+sinα（sinα-3）=-1（12分）
整理得：sinα+cosα=
2
3
①（5分）
1+sin2α-cos2α
1+tanα
=
2sin2α+2sinαcosα
1+
sinα
cosα

=
2sinαcosα(sinα+cosα)
sinα+cosα
=2sinαcosα（10分）
由①平方得1+2sinαcosα=
4
9
，∴2sinαcosα=-
5
9

即
1+sin2α-cos2α
1+tanα
=-
5
9
（12分）
练习册系列答案
相关题目
已知三点A、B、C的坐标分别为A(cosα，sinα)(α≠
kπ
4
，k∈Z)，B（3，0），C（0，3），若
AB
•
AC
=-1，求
1+sin2α-cos2α
1+tanα
的值．
已知三点A、B、C的坐标分别为（-1，0），（3，-1），（1，2），并且=，BF=，求证：∥.

已知三点A、B、C的坐标分别为A(3，0)，B(0，3)，C(cosα，sinα)，α≠，k∈Z，若=-1，求的值．

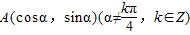已知三点A、B、C的坐标分别为，B（3，0），C（0，3），若，求的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网