题目内容
已知三点A、B、C的坐标分别为A(cosα,sinα)(α≠
,k∈Z),B(3,0),C(0,3),若
•
=-1,求
的值.
| kπ |
| 4 |
| AB |
| AC |
| 1+sin2α-cos2α |
| 1+tanα |
分析:直接求出向量
,
,利用
•
=-1,推出sinα+cosα=
,然后利用二倍角公式,以及切化弦整理所求表达式,通过sinα+cosα=
平方求出2sinαcosα=-
,得到结果.
| AB |
| AC |
| AB |
| AC |
| 2 |
| 3 |
| 2 |
| 3 |
| 5 |
| 9 |
解答:解:
=(3-cosα,-sinα),
=(-cosα,3-sinα)
∵
•
=-1,∴(cosα-3)•cosα+sinα(sinα-3)=-1(12分)
整理得:sinα+cosα=
①(5分)
=
=
=2sinαcosα(10分)
由①平方得1+2sinαcosα=
,∴2sinαcosα=-
即
=-
(12分)
| AB |
| AC |
∵
| AC |
| BC |
整理得:sinα+cosα=
| 2 |
| 3 |
| 1+sin2α-cos2α |
| 1+tanα |
| 2sin2α+2sinαcosα | ||
1+
|
=
| 2sinαcosα(sinα+cosα) |
| sinα+cosα |
由①平方得1+2sinαcosα=
| 4 |
| 9 |
| 5 |
| 9 |
即
| 1+sin2α-cos2α |
| 1+tanα |
| 5 |
| 9 |
点评:本题是中档题,以向量的数量积为载体,考查三角函数基本公式的应用,考查计算能力,转化思想.

练习册系列答案
相关题目
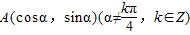 ,B(3,0),C(0,3),若
,B(3,0),C(0,3),若 ,求
,求 的值.
的值.