题目内容
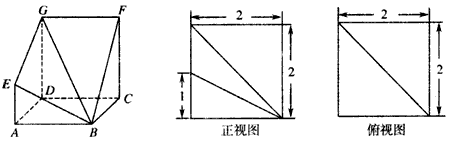
如图,多面体ABCDEF中,平面ADEF⊥平面ABCD,正方形ADEF的边长为2,直角梯形ABCD中,AB∥CD,AD⊥DC,AB=2,CD=4.(Ⅰ)求证:BC⊥平面BDE;
(Ⅱ)试在平面CDE上确定点P,欲使点P到直线DC、DE的距离相等,且AP与平面BEF所成的角等于30°.
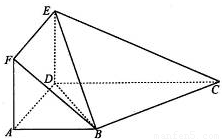
【答案】分析:(Ⅰ)欲证BC⊥平面BDE,根据直线与平面垂直的判定定理可知只需证BC与平面BDE内两相交直线垂直,根据面面垂直的性质可知ED⊥平面ABCD,则ED⊥BC,根据勾股定理可知BC⊥BD,满足定理所需条件;
(Ⅱ)DE,DA,DC两两垂直,以D为顶点,DA,DC,DE分别为x轴y轴z轴,建立直角坐标系D-xyz,求出D,A,E,B,F,以及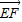 ,
,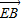 ,设P(o,y,z)通过|y|=|z|.设
,设P(o,y,z)通过|y|=|z|.设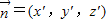 是平面BEF的法向量,利用
是平面BEF的法向量,利用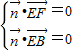 ,求出
,求出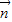 ,推出
,推出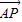 与
与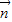 所成的角为60°或120°.通过cos
所成的角为60°或120°.通过cos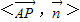 =
=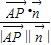 和y|=|z|.求出P的坐标.
和y|=|z|.求出P的坐标.
解答:解:(Ⅰ)在正方形ADEF中,ED⊥AD.
又因为平面ADEF⊥平面ABCD,且平面ADEF∩平面ABCD=AD,
所以ED⊥平面ABCD.
所以ED⊥BC.(3分)
在直角梯形ABCD中,AB=AD=1,CD=2,可得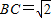 .
.
在△BCD中,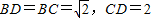 ,
,
所以BD2+BC2=CD2.
所以BC⊥BD.(5分)
所以BC⊥平面BDE.(6分)
(Ⅱ)DE,DA,DC两两垂直,以D为顶点,DA,DC,DE分别为x轴y轴z轴,建立直角坐标系D-xyz,
则D(0,0,0),A(2,0,0),E(0,0,2),B(2,2,0),F(2,0,2)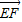 =(2,0,0),
=(2,0,0),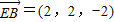 设P(o,y,z)则|y|=|z|.
设P(o,y,z)则|y|=|z|.
令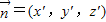 是平面BEF的法向量,则
是平面BEF的法向量,则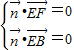 ,
,
∴
令y′=1,得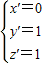
∴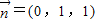
∵AP与平面BEF所成的角等于30°
∴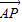 与
与 所成的角为60°或120°.
所成的角为60°或120°.
∴cos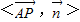 =
=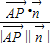 =
=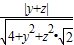 =
= .
.
∴y2+z2+4yz-4=0
又∵|y|=|z|.
∴y=z或y=-z,当y=z时y=z= ,
,
当y=-z时,上式无解,
∴P(0,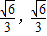 ),或P(0,-
),或P(0,-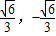 ).
).
点评:本题考查直线与平面垂直,直线与平面所成的角,空间向量的运算,考查空间想象能力,计算能力已经逻辑推理能力.
(Ⅱ)DE,DA,DC两两垂直,以D为顶点,DA,DC,DE分别为x轴y轴z轴,建立直角坐标系D-xyz,求出D,A,E,B,F,以及
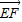 ,
,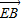 ,设P(o,y,z)通过|y|=|z|.设
,设P(o,y,z)通过|y|=|z|.设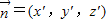 是平面BEF的法向量,利用
是平面BEF的法向量,利用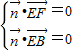 ,求出
,求出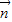 ,推出
,推出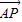 与
与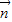 所成的角为60°或120°.通过cos
所成的角为60°或120°.通过cos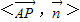 =
=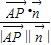 和y|=|z|.求出P的坐标.
和y|=|z|.求出P的坐标.解答:解:(Ⅰ)在正方形ADEF中,ED⊥AD.
又因为平面ADEF⊥平面ABCD,且平面ADEF∩平面ABCD=AD,
所以ED⊥平面ABCD.
所以ED⊥BC.(3分)
在直角梯形ABCD中,AB=AD=1,CD=2,可得
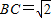 .
.在△BCD中,
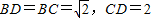 ,
,所以BD2+BC2=CD2.
所以BC⊥BD.(5分)
所以BC⊥平面BDE.(6分)
(Ⅱ)DE,DA,DC两两垂直,以D为顶点,DA,DC,DE分别为x轴y轴z轴,建立直角坐标系D-xyz,
则D(0,0,0),A(2,0,0),E(0,0,2),B(2,2,0),F(2,0,2)
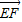 =(2,0,0),
=(2,0,0),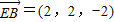 设P(o,y,z)则|y|=|z|.
设P(o,y,z)则|y|=|z|.令
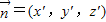 是平面BEF的法向量,则
是平面BEF的法向量,则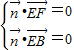 ,
,∴

令y′=1,得
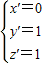
∴
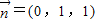
∵AP与平面BEF所成的角等于30°
∴
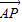 与
与 所成的角为60°或120°.
所成的角为60°或120°.∴cos
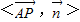 =
=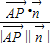 =
=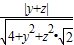 =
= .
.∴y2+z2+4yz-4=0
又∵|y|=|z|.
∴y=z或y=-z,当y=z时y=z=
 ,
,当y=-z时,上式无解,
∴P(0,
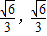 ),或P(0,-
),或P(0,-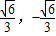 ).
).点评:本题考查直线与平面垂直,直线与平面所成的角,空间向量的运算,考查空间想象能力,计算能力已经逻辑推理能力.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目


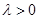 使得
使得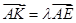 ,二面角A—BG—K的大小为
,二面角A—BG—K的大小为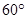 ,求
,求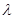 的值。
的值。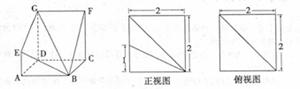
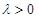 使得
使得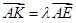 ,二面角A—BG—K的大小为
,二面角A—BG—K的大小为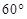 ,求
,求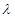 的值。
的值。
 使得
使得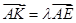 ,二面角A—BG—K的大小为
,二面角A—BG—K的大小为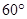 ,求
,求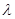 的值。
的值。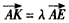 ,KF与平面ABG所成角为30°,求λ的值。
,KF与平面ABG所成角为30°,求λ的值。