题目内容
 如图,点F是椭圆
如图,点F是椭圆 的左焦点,A、B是椭圆的两个顶点,椭圆的离心率为
的左焦点,A、B是椭圆的两个顶点,椭圆的离心率为 .点C在x轴上,BC⊥BF,且B、C、F三点确定的圆M恰好与直线
.点C在x轴上,BC⊥BF,且B、C、F三点确定的圆M恰好与直线 相切.
相切.(Ⅰ)求椭圆的方程;
(Ⅱ)过F作一条与两坐标轴都不垂直的直线l交椭圆于P、Q两点,在x轴上是否存在定点N,使得NF恰好为△PNQ的内角平分线,若存在,求出点N的坐标,若不存在,请说明理由.
【答案】分析:(Ⅰ)从 =
= 着手分析a、b、c之间的关系,再结合条件BC⊥BF,且B、C、F三点确定的圆M恰好与直线
着手分析a、b、c之间的关系,再结合条件BC⊥BF,且B、C、F三点确定的圆M恰好与直线 相切,可求得a,从而可求得椭圆的方程;
相切,可求得a,从而可求得椭圆的方程;
(Ⅱ)假设在x轴上是否存在定点N,使得NF恰好为△PNQ的内角平分线,利用角平分线的性质定理得: =
= ,再结合椭圆的定义进行转化即可.
,再结合椭圆的定义进行转化即可.
解答:解:(Ⅰ)∵ =
= ,
,
∴c= a,b=
a,b= =
= a,
a,
又F(-c,0),B(0,b),在直角三角形BFO中,tan∠BFO= =
=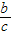 =
= ,
,
∴∠BFO= .|BF|=a.
.|BF|=a.
∵BC⊥BF,
∴∠BCF= ,
,
∴|CF|=2a.
∴B、C、F三点确定的圆M的圆心M的坐标为:( ,0),半径r=a;
,0),半径r=a;
又圆M与直线 相切,
相切,
∴圆心M到直线x+ y+3=0的距离等于r,即
y+3=0的距离等于r,即 =a,又a>0,
=a,又a>0,
∴a=2,
∴b= .
.
∴椭圆的方程为: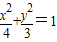 .
.
(Ⅱ)假设在x轴上是否存在定点N,使得NF恰好为△PNQ的内角平分线,
则由角平分线的性质定理得: =
= ,又|PF|+|PN|=2a=4,|QF|+|QN|=2a=4,
,又|PF|+|PN|=2a=4,|QF|+|QN|=2a=4,
∴ =
= ,
,
∴|PF|=|QF|,即F为PQ的中点,
∴PQ⊥x轴,这与已知“过F作一条与两坐标轴都不垂直的直线l交椭圆于P、Q两点”矛盾,
∴假设不成立,即在x轴上不存在定点N,使得NF恰好为△PNQ的内角平分线.
点评:本题考查直线与圆锥曲线的综合问题,求椭圆的方程,关键在于根据题意从角入手分析出a、b、c之间的关系,难点在于(Ⅱ)中椭圆定义的灵活应用,属于难题.
 =
= 着手分析a、b、c之间的关系,再结合条件BC⊥BF,且B、C、F三点确定的圆M恰好与直线
着手分析a、b、c之间的关系,再结合条件BC⊥BF,且B、C、F三点确定的圆M恰好与直线 相切,可求得a,从而可求得椭圆的方程;
相切,可求得a,从而可求得椭圆的方程;(Ⅱ)假设在x轴上是否存在定点N,使得NF恰好为△PNQ的内角平分线,利用角平分线的性质定理得:
 =
= ,再结合椭圆的定义进行转化即可.
,再结合椭圆的定义进行转化即可.解答:解:(Ⅰ)∵
 =
= ,
,∴c=
 a,b=
a,b= =
= a,
a,又F(-c,0),B(0,b),在直角三角形BFO中,tan∠BFO=
 =
=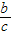 =
= ,
,∴∠BFO=
 .|BF|=a.
.|BF|=a.∵BC⊥BF,
∴∠BCF=
 ,
,∴|CF|=2a.
∴B、C、F三点确定的圆M的圆心M的坐标为:(
 ,0),半径r=a;
,0),半径r=a;又圆M与直线
 相切,
相切,∴圆心M到直线x+
 y+3=0的距离等于r,即
y+3=0的距离等于r,即 =a,又a>0,
=a,又a>0,∴a=2,
∴b=
 .
.∴椭圆的方程为:
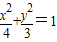 .
.(Ⅱ)假设在x轴上是否存在定点N,使得NF恰好为△PNQ的内角平分线,
则由角平分线的性质定理得:
 =
= ,又|PF|+|PN|=2a=4,|QF|+|QN|=2a=4,
,又|PF|+|PN|=2a=4,|QF|+|QN|=2a=4,∴
 =
= ,
,∴|PF|=|QF|,即F为PQ的中点,
∴PQ⊥x轴,这与已知“过F作一条与两坐标轴都不垂直的直线l交椭圆于P、Q两点”矛盾,
∴假设不成立,即在x轴上不存在定点N,使得NF恰好为△PNQ的内角平分线.
点评:本题考查直线与圆锥曲线的综合问题,求椭圆的方程,关键在于根据题意从角入手分析出a、b、c之间的关系,难点在于(Ⅱ)中椭圆定义的灵活应用,属于难题.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
 如图,点F是椭圆
如图,点F是椭圆 的左焦点,A、B是椭圆的两个顶点,椭圆的离心率为
的左焦点,A、B是椭圆的两个顶点,椭圆的离心率为 .点C在x轴上,BC⊥BF,且B、C、F三点确定的圆M恰好与直线
.点C在x轴上,BC⊥BF,且B、C、F三点确定的圆M恰好与直线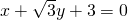 相切.
相切.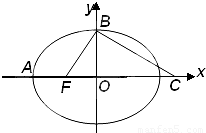 如图,点F是椭圆
如图,点F是椭圆 的左焦点,A、B是椭圆的两个顶点,椭圆的离心率为
的左焦点,A、B是椭圆的两个顶点,椭圆的离心率为 .点C在x轴上,BC⊥BF,且B、C、F三点确定的圆M恰好与直线
.点C在x轴上,BC⊥BF,且B、C、F三点确定的圆M恰好与直线 相切.
相切. 的左焦点,直线l为对应的准线,直线l与x轴交于P点,线段MN为椭圆的长轴,已知|MN|=8,且|PM|=2|MF|.
的左焦点,直线l为对应的准线,直线l与x轴交于P点,线段MN为椭圆的长轴,已知|MN|=8,且|PM|=2|MF|.