题目内容
8.椭圆$\frac{x^2}{13}+\frac{y^2}{4}=1$的焦点为F1,F2,点P是椭圆上的动点,当∠F1PF2为钝角时,点P的横坐标的取值范围是$(-\frac{{\sqrt{65}}}{3},\frac{{\sqrt{65}}}{3})$.分析 设P(x,y),则$\frac{x^2}{13}+\frac{y^2}{4}=1$,可得y2=4$(1-\frac{{x}^{2}}{13})$.由于∠F1PF2为钝角,可得$\overrightarrow{P{F}_{1}}•\overrightarrow{P{F}_{2}}$<0,解出即可.
解答 解:由椭圆的标准方程可得:a2=13,b=2,
∴$c=\sqrt{{a}^{2}-{b}^{2}}$=3.
F1(-3,0),F2(3,0).
设P(x,y),则$\frac{x^2}{13}+\frac{y^2}{4}=1$,
∴y2=4$(1-\frac{{x}^{2}}{13})$.
∵∠F1PF2为钝角,
∴$\overrightarrow{P{F}_{1}}•\overrightarrow{P{F}_{2}}$=(x+3,y)•(x-3,y)=x2-9+y2<0,
∴x2-9+4$(1-\frac{{x}^{2}}{13})$<0.
化为x2$<\frac{65}{9}$,
解得$-\frac{\sqrt{65}}{3}$<x<$\frac{\sqrt{65}}{3}$.
∴点P的横坐标的取值范围是$(-\frac{{\sqrt{65}}}{3},\frac{{\sqrt{65}}}{3})$,
故答案为:$(-\frac{{\sqrt{65}}}{3},\frac{{\sqrt{65}}}{3})$.
点评 本题考查了椭圆的标准方程及其性质、向量夹角公式与数量积运算性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
19.已知f(x)=$\left\{\begin{array}{l}(2a-1)x+3a,x<1\\{a^x},x≥1\end{array}$满足对任意x1≠x2都有$\frac{{f({x_1})-f({x_2})}}{{{x_1}-{x_2}}}$<0成立,那么a的取值范围是( )
| A. | (0,1) | B. | $(0,\frac{1}{2})$ | C. | $[\frac{1}{4},\frac{1}{2})$ | D. | $[\frac{1}{4},1)$ |
13.根据如图所示的算法语句,可知输出的结果S是( )
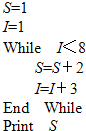
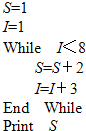
| A. | 11 | B. | 9 | C. | 7 | D. | 5 |
17.若cos2θ+2msinθ-2m-2<0对θ∈R恒成立,则实数m的取值范围是( )
| A. | m<1-$\sqrt{2}$ | B. | m>1-$\sqrt{2}$ | C. | 1-$\sqrt{2}$<m<1+$\sqrt{2}$ | D. | 1-$\sqrt{2}$<m≤1 |
 如图,已知正方形ABCD和矩形ACEF所在平面互相垂直,AB=$\sqrt{2}$,AF=1,M是线段EF的中点.用向量方法证明与解答:
如图,已知正方形ABCD和矩形ACEF所在平面互相垂直,AB=$\sqrt{2}$,AF=1,M是线段EF的中点.用向量方法证明与解答: