题目内容
已知函数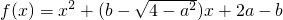 是偶函数,则函数图象与y轴交点的纵坐标的最大值是
是偶函数,则函数图象与y轴交点的纵坐标的最大值是
- A.-4
- B.2
- C.3
- D.4
D
分析:因为f(x)为二次函数,故f(x)为偶函数时,对称轴为x=0,可求出a和b的关系.
而f(x)图象与y轴交点的纵坐标是f(0)=2a-b,数形结合求最值即可.
解答: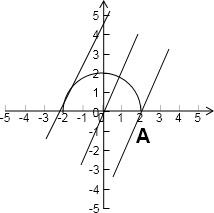 解:由f(x)为偶函数可得
解:由f(x)为偶函数可得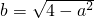 ,
,
它表示以原点为圆心,以2为半径的上半圆;
f(x)图象与y轴交点的纵坐标是f(0)=2a-b,
令t=2a-b,则b=2a-t,它表示斜率为2的直线.
如图:当直线过点A(2,0)时,
在y轴上的截距-t最小,从而t最大,值为4
故选D.
点评:本题考查函数奇偶性的应用、数形结合求最值,有一定的综合性,能力要求较高.
分析:因为f(x)为二次函数,故f(x)为偶函数时,对称轴为x=0,可求出a和b的关系.
而f(x)图象与y轴交点的纵坐标是f(0)=2a-b,数形结合求最值即可.
解答:
 解:由f(x)为偶函数可得
解:由f(x)为偶函数可得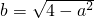 ,
,它表示以原点为圆心,以2为半径的上半圆;
f(x)图象与y轴交点的纵坐标是f(0)=2a-b,
令t=2a-b,则b=2a-t,它表示斜率为2的直线.
如图:当直线过点A(2,0)时,
在y轴上的截距-t最小,从而t最大,值为4
故选D.
点评:本题考查函数奇偶性的应用、数形结合求最值,有一定的综合性,能力要求较高.

练习册系列答案
 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
 是偶函数,则此函数的图象与y轴交点的纵坐标的最大值为( )
是偶函数,则此函数的图象与y轴交点的纵坐标的最大值为( ) B.2 C.4
D.-2
B.2 C.4
D.-2 是偶函数,则函数图象与y轴交点的纵坐标的最大值是 .
是偶函数,则函数图象与y轴交点的纵坐标的最大值是 . 是偶函数,则函数图象与y轴交点的纵坐标的最大值是 .
是偶函数,则函数图象与y轴交点的纵坐标的最大值是 . 是偶函数,则
是偶函数,则 的值等于( )
的值等于( ) 是偶函数,则函数图像与
是偶函数,则函数图像与 轴交点的纵坐标的最大值是______.
轴交点的纵坐标的最大值是______.