题目内容
(
南京陶吴中学模拟)如下图，在四棱锥P—ABCD中，△PBC为正三角形，AB⊥平面PBC，AB∥CD，AB=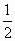
DC，E为PD的中点．
(1)
求证：AE∥平面PBC；(2)
求证：AE⊥平面PDC；(3)
若AB=BP=2，求四棱锥P—ABCD的体积．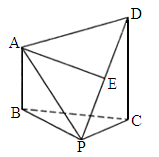
答案：略
解析：
解析：
|
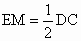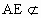解析： (1)证明：取PC的中点M，连接EM，则EM∥CD， ，所以有EM∥AB且EM=AB，则四边形ABME是平行四边形．所以AE∥BM，又因为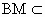 平面PBC， 平面PBC，所以AE∥平面PBC．
(2) 因为AB⊥平面PBC，AB∥CD，所以CD⊥平面PBC，CD⊥BM．由(1)得，BM⊥PC，所以BM⊥平面PDC，又AE∥BM，所以AE⊥平面PDC．(3) 取BC的中点O，连接PO，则PO⊥BC．AB⊥平面PBC，PO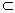 平面PBC，∴AB⊥PO，又PO⊥BC，AB∩BC=B，∴PO⊥平面ABCD，
∴  ．
∵  ， ，
∴  ． |
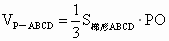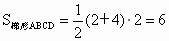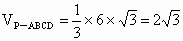练习册系列答案
阅读快车系列答案
相关题目
α，则l∥β；
α．n