题目内容
已知函数 .
.(1)如果f(x)存在零点,求a的取值范围;
(2)是否存在常数a,使f(x)为奇函数?如果存在,求a的值,如果不存在,说明理由.
【答案】分析:(1)若f(x)存在零点,即f(x)=a-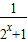 =0,推出a=
=0,推出a= ,从而求出a的范围;
,从而求出a的范围;
(2)假设存在,函数f(x)定义域为R,f(x)为奇函数可得f(0)=0,可得a的值,求出f(x)的解析式;
解答:解:(1)令f(x)=0得 ,
,
由于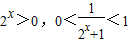
欲使f(x)有零点,a∈(0,1)
(2)易知函数f(x)定义域为R.
如果f(x)为奇函数,则f(0)=0,可得
此时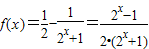
∴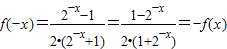 ,
,
所以,当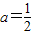 时f(x)为奇函数;
时f(x)为奇函数;
点评:此题主要考查指数函数的性质及其应用,第二问涉及奇函数的性质,是一道基础题;
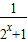 =0,推出a=
=0,推出a= ,从而求出a的范围;
,从而求出a的范围;(2)假设存在,函数f(x)定义域为R,f(x)为奇函数可得f(0)=0,可得a的值,求出f(x)的解析式;
解答:解:(1)令f(x)=0得
 ,
,由于
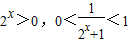
欲使f(x)有零点,a∈(0,1)
(2)易知函数f(x)定义域为R.
如果f(x)为奇函数,则f(0)=0,可得

此时
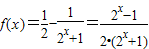
∴
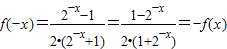 ,
,所以,当
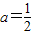 时f(x)为奇函数;
时f(x)为奇函数;点评:此题主要考查指数函数的性质及其应用,第二问涉及奇函数的性质,是一道基础题;

练习册系列答案
相关题目
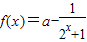 .
. ,
, .
. 在
在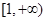 上是单调减函数,求
上是单调减函数,求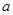 的取值范围;
的取值范围; ,使得方程
,使得方程 在区间
在区间 内有且只有两个不相等的实数根?若存在,请求出
内有且只有两个不相等的实数根?若存在,请求出 .
. ,求
,求 的单调区间和极值;
的单调区间和极值; ,函数
,函数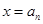 处取得极值.
处取得极值.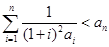 ;
; .
.  ,
, .
. 在
在 上是单调增函数,求
上是单调增函数,求 的取值范围;
的取值范围;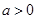 ,使得方程
,使得方程 在区间
在区间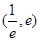 内有且只
内有且只