题目内容
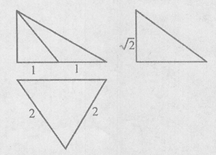
若某多面体的三视图(单位: cm) 如图所示, 则此多面体外接球的表面积是
| A．cm2 | B． cm2 | C．cm2 | D．cm2 |
B
专题：计算题．
分析：画出三视图复原后几何体是正方体去掉一个角后的几何体，如图，推断出几何体的外接球的直径，直接求出几何体的外接球的表面积．
解答：解：三视图复原几何体如图：
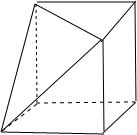
是正方体去掉一个角后的几何体，
它的外接球就是展开为正方体的外接球，外接球的直径就是正方体的体对角线的长度，
体对角线的长度为：
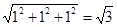，所以外接球的半径为：
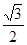；所以外接球的表面积为：4π(
)
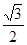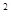=3π．故选B．
点评：本题考查由三视图复原几何体的空间想象能力，几何体的外接球的半径的求解是解题的关键，考查逻辑思维能力，计算能力．三视图复原几何体与几何体的三视图的关系必须多练习多思考，才能解题得心应手．
练习册系列答案
相关题目
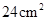，它的顶点都在一个球面上，则这个球的表面积是_________
。
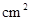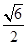
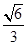
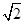
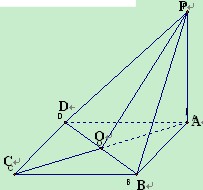
，则此球的体积为 ．
