题目内容
在锐角三角形ABC中，已知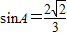
，AD是BC边上的高，AD=
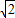，BC=2．（1）求：
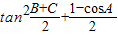的值（2）求证：点D是BC的中点．
【答案】分析：（1）在△ABC为锐角三角形中，求出 
，利用半角公式可得原式=
．
（2）设DC=x，∠CAD=α，∠BAD=β，求出tanα和 tanβ的解析式，由
，求得x=1，即得
点D为BC的中点．
解答：解：（1）∵△ABC为锐角三角形
，∴
，
原式=
．
（2）证明：设DC=x，∠CAD=α，∠BAD=β
则
，∵
，
∴
，∴点D为BC的中点．
点评：本题考查同角三角函数的基本关系，半角公式的应用，直角三角形中的边角关系，求出
，
是解题的关键．
，利用半角公式可得原式=．（2）设DC=x，∠CAD=α，∠BAD=β，求出tanα和 tanβ的解析式，由
，求得x=1，即得点D为BC的中点．
解答：解：（1）∵△ABC为锐角三角形
，∴，原式=
．（2）证明：设DC=x，∠CAD=α，∠BAD=β
则
，∵，∴
，∴点D为BC的中点．点评：本题考查同角三角函数的基本关系，半角公式的应用，直角三角形中的边角关系，求出
，是解题的关键．
练习册系列答案
相关题目