题目内容
有下列命题:①函数y=cos(
 x+
x+ )是奇函数;
)是奇函数;②函数f(x)=4sin
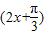 的表达式可改写为f(x)=4cos
的表达式可改写为f(x)=4cos ;
;③若α、β是第一象限角且α<β,则tan α<tan β;
④函数y=sin(2x+
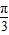 )的图象关于直线x=
)的图象关于直线x= 成轴对称图形.
成轴对称图形.其中正确的是 (把你认为正确的命题序号都填上)
【答案】分析:①利用诱导公式将函数进行化简,然后判断函数的奇偶性.②利用诱导公式进行化简判断.③利用正切函数的性质判断.④利用三角函数的图象和性质判断.
解答:解:①因为y=cos( x+
x+ )=-sin
)=-sin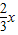 ,为奇函数,所以①正确.
,为奇函数,所以①正确.
②函数f(x)=4sin =
=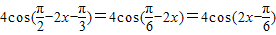 ,所以②正确.
,所以②正确.
③因为函数在定义域内部单调,所以③错误.
④当x= 时,
时,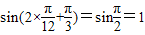 ,所以直线x=
,所以直线x=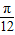 是函数的一条对称轴,所以④正确.
是函数的一条对称轴,所以④正确.
故答案为:①②④.
点评:本题主要考查诱导公式以及三角函数的图象和性质.综合性较强.
解答:解:①因为y=cos(
 x+
x+ )=-sin
)=-sin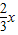 ,为奇函数,所以①正确.
,为奇函数,所以①正确.②函数f(x)=4sin
 =
=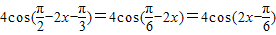 ,所以②正确.
,所以②正确.③因为函数在定义域内部单调,所以③错误.
④当x=
 时,
时,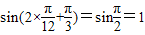 ,所以直线x=
,所以直线x=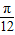 是函数的一条对称轴,所以④正确.
是函数的一条对称轴,所以④正确.故答案为:①②④.
点评:本题主要考查诱导公式以及三角函数的图象和性质.综合性较强.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目