题目内容
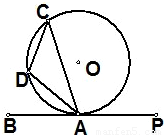 如图,已知PB是⊙O的切线,A是切点,D是弧AC上一点,若∠BAC=70°,则∠ADC= .
如图,已知PB是⊙O的切线,A是切点,D是弧AC上一点,若∠BAC=70°,则∠ADC= .
【答案】分析:由PB是⊙O的切线得:∠DAB=∠ACD,从而在三角形ACD中即可求得∠ADC.
解答:解:∵∠DAB=∠ACD,∠BAC=∠DAB+∠CAD=70°,
从而∠ACD+∠CAD=70°,
∴∠ADC=180°-70°=110°.
故答案为:110°.
点评:本小题主要考查弦切角、弦切角的应用、圆的切线等基础知识.属于基础题.
解答:解:∵∠DAB=∠ACD,∠BAC=∠DAB+∠CAD=70°,
从而∠ACD+∠CAD=70°,
∴∠ADC=180°-70°=110°.
故答案为:110°.
点评:本小题主要考查弦切角、弦切角的应用、圆的切线等基础知识.属于基础题.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
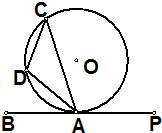 15、如图,已知PB是⊙O的切线,A是切点,D是弧AC上一点,若∠BAC=70°,则∠ADC=
15、如图,已知PB是⊙O的切线,A是切点,D是弧AC上一点,若∠BAC=70°,则∠ADC=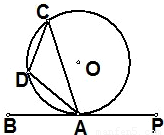 如图,已知PB是⊙O的切线,A是切点,D是弧AC上一点,若∠BAC=70°,则∠ADC= .
如图,已知PB是⊙O的切线,A是切点,D是弧AC上一点,若∠BAC=70°,则∠ADC= .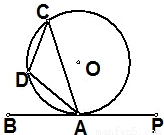 如图,已知PB是⊙O的切线,A是切点,D是弧AC上一点,若∠BAC=70°,则∠ADC= .
如图,已知PB是⊙O的切线,A是切点,D是弧AC上一点,若∠BAC=70°,则∠ADC= .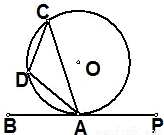 如图,已知PB是⊙O的切线,A是切点,D是弧AC上一点,若∠BAC=70°,则∠ADC= .
如图,已知PB是⊙O的切线,A是切点,D是弧AC上一点,若∠BAC=70°,则∠ADC= .