题目内容
15.利用计算机随机在[0,4]上先后取两个数分别记为x,y,在平面直角坐标系中,点P的坐标为(x-3,x-y),则P点在第一象限的概率是$\frac{7}{32}$.分析 由题意,画出图形,随机在[0,4]上先后取两个数分别记为x,y,对应区域为边长为4 的正方形,满足P点在第一象限是区域$\left\{\begin{array}{l}{x-3>0}\\{x-y>0}\end{array}\right.$,分别求出面积,利用几何概型公式求值.
解答 解:由题意,x,y∈[0,4],在平面直角坐标系中,点P的坐标为(x-3,x-y),
则P点在第一象限,则$\left\{\begin{array}{l}{x-3>0}\\{x-y>0}\end{array}\right.$,如图 满足条件如图阴影部分,
满足条件如图阴影部分,
由几何概型的公式可得$\frac{1×4-\frac{1}{2}}{4×4}=\frac{7}{32}$;
故答案为:$\frac{7}{32}$
点评 本题考查了几何概型的公式的运用;关键是明确满足条件的区域面积,利用几何概型公式解答.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目

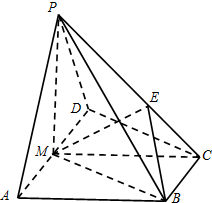 如图,在四棱锥P-ABCD中,侧面PAD是正三角形,底面ABCD直角梯形,AD∥BC,∠ADC=90°,AD=2BC=2,$CD=\sqrt{3}$,平面PAD⊥底面ABCD,若M为AD的中点.
如图,在四棱锥P-ABCD中,侧面PAD是正三角形,底面ABCD直角梯形,AD∥BC,∠ADC=90°,AD=2BC=2,$CD=\sqrt{3}$,平面PAD⊥底面ABCD,若M为AD的中点.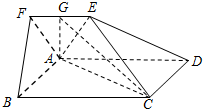 如图,在五面体ABCDEF中,四边形ABCD为正方形,EF∥AD,平面ADEF⊥平面ABCD,且BC=2EF,AE=AF,点G是EF的中点.
如图,在五面体ABCDEF中,四边形ABCD为正方形,EF∥AD,平面ADEF⊥平面ABCD,且BC=2EF,AE=AF,点G是EF的中点. 中,
中, ,
,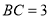 ,
, ,
, 是
是 上的点,则
上的点,则 到
到 的距离的乘积的最大值为( )
的距离的乘积的最大值为( ) D.9
D.9