题目内容
考察下列式子:
 ,得出的一般性结论为________________________
,得出的一般性结论为________________________
【答案】
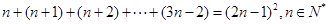
【解析】
试题分析:由1=12=(2×1-1)2;
2+3+4=32=(2×2-1)2;
3+4+5+6+7=52=(2×3-1)2;
4+5+6+7+8+9+10=72=(2×4-1)2;
………
由上边的式子可以得出:第n个等式的左边的第一项为n,接下来依次加1,共有2n-1项,等式右边是2n-1的平方,
从而我们可以得出的一般性结论为:n+(n+1)+…+(2n-1)+…+(3n-2)=(2n-1)2(n∈N*)。
考点:本题主要考查归纳推理。
点评:归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).解题时要注意观察,善于总结.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
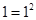 ;
;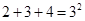 ;
;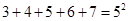 ;
;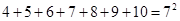 ;
; 得出的结论是 .
得出的结论是 .