题目内容
在二项式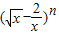 的展开式中,各项的二项式系数之和与各项系数和之比为64.( n∈N*)
的展开式中,各项的二项式系数之和与各项系数和之比为64.( n∈N*)(1)求n值;
(2)求展开式中的常数项.
【答案】分析:(1)各项的二项式系数之和为2n ,令x=1可得各项系数和为(-1)n ,由2n:(-1)n=64 可得n的值.
(2)根据通项公式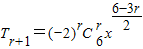 ,由6-3r=0得r=2,从而得到常数项.
,由6-3r=0得r=2,从而得到常数项.
解答:解:(1)各项的二项式系数之和为2n ,令x=1可得各项系数和为(-1)n ,
由2n:(-1)n=64 可得(-2)n=64,∴n=6. (6分)
(2)由(1)知,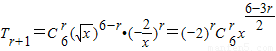 ,(10分)
,(10分)
由6-3r=0得r=2,∴展开式中的常数项为(-2)2C62=60. (13分)
点评:本题主要考查二项式定理,二项展开式的通项公式,求展开式中某项的系数,注意各项的二项式系数之和与各项系数和的区别.
(2)根据通项公式
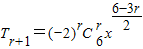 ,由6-3r=0得r=2,从而得到常数项.
,由6-3r=0得r=2,从而得到常数项.解答:解:(1)各项的二项式系数之和为2n ,令x=1可得各项系数和为(-1)n ,
由2n:(-1)n=64 可得(-2)n=64,∴n=6. (6分)
(2)由(1)知,
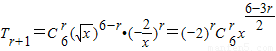 ,(10分)
,(10分)由6-3r=0得r=2,∴展开式中的常数项为(-2)2C62=60. (13分)
点评:本题主要考查二项式定理,二项展开式的通项公式,求展开式中某项的系数,注意各项的二项式系数之和与各项系数和的区别.

练习册系列答案
相关题目


 的展开式中,含
的展开式中,含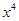 的项的系数是
的项的系数是  的展开式中,含
的展开式中,含 的项的系数是
的项的系数是