题目内容
【题目】设函数![]() (是常数).
(是常数).
(1)证明:![]() 是奇函数;
是奇函数;
(2)当![]() 时,证明:
时,证明:![]() 在区间
在区间![]() 上单调递增;
上单调递增;
(3)若![]() ,使得
,使得![]() ,求实数m的取值范围.
,求实数m的取值范围.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)可看出f(x)的定义域为{x|x≠0},并容易求出f(﹣x)=﹣f(x),从而得出f(x)是奇函数;
(2)λ=1时,![]() ,根据增函数的定义:设任意的x1>x2>1,然后作差,通分,提取公因式,说明f(x1)>f(x2)即可得出f(x)在(1,+∞)上单调递增;
,根据增函数的定义:设任意的x1>x2>1,然后作差,通分,提取公因式,说明f(x1)>f(x2)即可得出f(x)在(1,+∞)上单调递增;
(3)可设![]() ,根据题意可知,m≥g(x)min,x∈[1,2],可设2x=t(2≤t≤4),得出
,根据题意可知,m≥g(x)min,x∈[1,2],可设2x=t(2≤t≤4),得出![]() ,根据上面知y
,根据上面知y![]() 在[2,4]上单调递增,从而可求出g(x)在[1,2]上的最小值,即得出m的范围.
在[2,4]上单调递增,从而可求出g(x)在[1,2]上的最小值,即得出m的范围.
解:(1)定义域为{x|x≠0},且f(﹣x)![]() ,
,
∴f(x)是奇函数;
(2)证明:λ=1时,![]() ,
,
设x1>x2>1,则: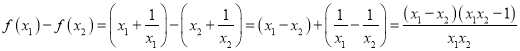 ,
,
∵x1>x2>1,
∴x1﹣x2>0,x1x2﹣1>0,x1x2>0,
∴![]() ,
,
∴f(x1)>f(x2),
∴f(x)在区间(1,+∞)上单调递增;
(3)设![]() ,
,
x∈[1,2],使得![]() 等价于m≥g(x)min,x∈[1,2],
等价于m≥g(x)min,x∈[1,2],
设2x=t(2≤t≤4),则![]() ,由(2)可知,
,由(2)可知,![]() 在[2,4]上单调递增,
在[2,4]上单调递增,
∴当t=2,即x=1时,y取得最小值为![]() ,
,
∴![]() ,
,
∴实数m的取值范围为![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】已知表1和表2是某年部分日期的天安门广场升旗时刻表:
表1:某年部分日期的天安门广场升旗时刻表
日期 | 升旗时刻 | 日期 | 升旗时刻 | 日期 | 升旗时刻 | 日期 | 升旗时刻 |
1月1日 | 7:36 | 4月9日 | 5:46 | 7月9日 | 4:53 | 10月8日 | 6:17 |
1月21日 | 7:11 | 4月28日 | 5:19 | 7月27日 | 5:07 | 10月26日 | 6:36 |
2月10日 | 7:14 | 5月16日 | 4:59 | 8月14日 | 5:24 | 11月13日 | 6:56 |
3月2日 | 6:47 | 6月3日 | 4:47 | 9月2日 | 5:42 | 12月1日 | 7:16 |
3月22日 | 6:15 | 6月22日 | 4:46 | 9月20日 | 5:50 | 12月20日 | 7:31 |
表2:某年1月部分日期的天安门广场升旗时刻表
日期 | 升旗时刻 | 日期 | 升旗时刻 | 日期 | 升旗时刻 |
2月1日 | 7:23 | 2月11日 | 7:13 | 2月21日 | 6:59 |
2月3日 | 7:22 | 2月13日 | 7:11 | 2月23日 | 6:57 |
2月5日 | 7:20 | 2月15日 | 7:08 | 2月25日 | 6:55 |
2月7日 | 7:17 | 2月17日 | 7:05 | 2月27日 | 6:52 |
2月9日 | 7:15 | 2月19日 | 7:02 | 2月28日 | 6:49 |
(1)从表1的日期中随机选出一天,试估计这一天的升旗时刻早于7:00的概率;
(2)甲、乙二人各自从表2的日期中随机选择一天观看升旗,且两人的选择相互独立,记![]() 为这两人中观看升旗的时刻早于7:00的人数,求
为这两人中观看升旗的时刻早于7:00的人数,求![]() 的 分布列和数学期望;
的 分布列和数学期望;
(3)将表1和表2的升旗时刻化为分数后作为样本数据(如7:31化为![]() ),记表2中所有升旗时刻对应数据的方差为
),记表2中所有升旗时刻对应数据的方差为![]() ,表1和表2中所有升旗时刻对应数据的方差为
,表1和表2中所有升旗时刻对应数据的方差为![]() ,判断
,判断![]() 与
与![]() 的大小(只需写出结论).
的大小(只需写出结论).