题目内容
若函数f（x）=lg（x2-ax-3）在（-∞，-1 ）上是减函数，则a的取值范围是________．
[2，+∞）
分析：由题意可得 y=x2-ax-3在（-∞，-1 ）上是减函数，且y＞0；故有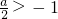
，且1+a-3≥0．解不等式求得
a的取值范围．
解答：由题意可得 y=x2-ax-3在（-∞，-1 ）上是减函数，且y＞0．
故有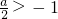，且1+a-3≥0．
解得 a≥2，故a的取值范围是[2，+∞），
故答案为：[2，+∞）．
点评：本题主要考查对数函数的单调性和特殊点，体现了转化的数学思想，得到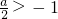，且1+a-3≥0，是解题的关键．
分析：由题意可得 y=x2-ax-3在（-∞，-1 ）上是减函数，且y＞0；故有
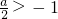，且1+a-3≥0．解不等式求得a的取值范围．
解答：由题意可得 y=x2-ax-3在（-∞，-1 ）上是减函数，且y＞0．
故有
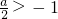，且1+a-3≥0．解得 a≥2，故a的取值范围是[2，+∞），
故答案为：[2，+∞）．
点评：本题主要考查对数函数的单调性和特殊点，体现了转化的数学思想，得到
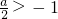，且1+a-3≥0，是解题的关键． 
练习册系列答案
开心练习课课练与单元检测系列答案
相关题目
给出下列命题：