题目内容
若定义在区间D上的函数y=f(x)对于区间D上任意x1,x2都有不等式
[f(x1)+f(x2)]≤f(
)成立,则称函数y=f(x)在区间D上的凸函数.
(I)证明:定义在R上的二次函数f(x)=ax2+bx+c(a<0)是凸函数;
(II)对(I)的函数y=f(x),若|f(1)|≤1,|f(2)|≤2,|f(3)|≤3,求|f(4)|取得最大值时函数y=f(x)的解析式;
(III)定义在R上的任意凸函数y=f(x),当q,p,m,n∈N*且p<m<n<q,p+q=m+n,证明:f(p)+f(q)≤f(m)+f(n).
| 1 |
| 2 |
| x1+x2 |
| 2 |
(I)证明:定义在R上的二次函数f(x)=ax2+bx+c(a<0)是凸函数;
(II)对(I)的函数y=f(x),若|f(1)|≤1,|f(2)|≤2,|f(3)|≤3,求|f(4)|取得最大值时函数y=f(x)的解析式;
(III)定义在R上的任意凸函数y=f(x),当q,p,m,n∈N*且p<m<n<q,p+q=m+n,证明:f(p)+f(q)≤f(m)+f(n).
分析:(I)利用凸函数的定义,验证函数f(x)=ax2+bx+c(a<0)满足不等式
[f(x1)+f(x2)]≤f(
)成立.
(II)根据已知条件得到a,b,c满足的不等式,将f(4)用f(1),f(2),f(3)表示,从而得到f(4)取最大值时a,b,d 值.
(III)结合凸函数的定义以及梯形的中位线公式得到要证的不等式.
| 1 |
| 2 |
| x1+x2 |
| 2 |
(II)根据已知条件得到a,b,c满足的不等式,将f(4)用f(1),f(2),f(3)表示,从而得到f(4)取最大值时a,b,d 值.
(III)结合凸函数的定义以及梯形的中位线公式得到要证的不等式.
解答:解:(I)证明:对任意x1,x2∈R,当a<0,
有[f(x1)+f(x2)]-2f(
)=ax12+bx1+c+ax22+bx2+c-2[a(
)2+b(
)+c]=ax12+ax22-
a(x12+x22+2x1x2)=
a(x1-x2)2 (3分)
∴当a<0时,f(x1)+f(x2)≤2f(
),即
≤f(
)
当a<0时,函数f(x)是凸函数.
(2)因为|f(1)|≤1,|f(2)|≤2,|f(3)|≤3,
所以
,
又f(4)=16a+4b+c
设16a+4b+c=x(a+b+c)+y(4a+2b+c)+z(9a+3b+c)
所以
解得x=1,y=-3,z=3
所以f(4)=f(1)-3f(2)+3f(3)
所以-16≤f(4)≤16
所以f(4)的最大值为16
当
取得
解得a=4,b=-15,c=12,
(III)因为p<m<n<q,p+q=m+n,y=f(x)为凸函数,
所以f(p)+f(q)≤2f(p+q)=2f(m+n)
f(m)+f(n))≤2f(m+n)
因为y=f(x)为凸函数,
所以f(p)+f(q)≤f(m)+f(n).
有[f(x1)+f(x2)]-2f(
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴当a<0时,f(x1)+f(x2)≤2f(
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
当a<0时,函数f(x)是凸函数.
(2)因为|f(1)|≤1,|f(2)|≤2,|f(3)|≤3,
所以
|
又f(4)=16a+4b+c
设16a+4b+c=x(a+b+c)+y(4a+2b+c)+z(9a+3b+c)
所以
|
解得x=1,y=-3,z=3
所以f(4)=f(1)-3f(2)+3f(3)
所以-16≤f(4)≤16
所以f(4)的最大值为16
当
|
解得a=4,b=-15,c=12,
(III)因为p<m<n<q,p+q=m+n,y=f(x)为凸函数,
所以f(p)+f(q)≤2f(p+q)=2f(m+n)
f(m)+f(n))≤2f(m+n)
因为y=f(x)为凸函数,
所以f(p)+f(q)≤f(m)+f(n).
点评:本题是一定新定义的题,考查了不等式的性质及二次函数的性质、待定系数法求函数的定义域.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目

 的单调性;
的单调性;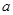 的取值范围;
的取值范围;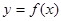 对于区间D上的任意两个值x1、x2总有以下不等式
对于区间D上的任意两个值x1、x2总有以下不等式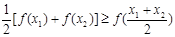 成立,则称函数
成立,则称函数 ,试判断函数
,试判断函数 ,
, 成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”.
成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”. ,
, 成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”.
成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”.