题目内容
已知向量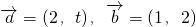 ,若t=t1时,
,若t=t1时, ∥
∥ ;t=t2时,
;t=t2时, ,则
,则
- A.t1=-4,t2=-1
- B.t1=-4,t2=1
- C.t1=4,t2=-1
- D.t1=4,t2=1
C
分析:题目所给的条件既有平行又有垂直,根据平行和垂直的坐标形式的充要条件,写出方程,解出其中的变量,就是我们要求的结果.
解答:向量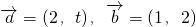 ,
,
若t=t1时, ∥
∥ ,
,
∴t1=4;t=t2时, ,t2=-1,
,t2=-1,
故选C.
点评:认识向量的代数特性.向量的坐标表示,实现了“形”与“数”的互相转化.以向量为工具,几何问题可以代数化,代数问题可以几何化.
分析:题目所给的条件既有平行又有垂直,根据平行和垂直的坐标形式的充要条件,写出方程,解出其中的变量,就是我们要求的结果.
解答:向量
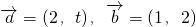 ,
,若t=t1时,
 ∥
∥ ,
,∴t1=4;t=t2时,
 ,t2=-1,
,t2=-1,故选C.
点评:认识向量的代数特性.向量的坐标表示,实现了“形”与“数”的互相转化.以向量为工具,几何问题可以代数化,代数问题可以几何化.

练习册系列答案
相关题目
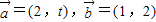 ,若t=t1时,
,若t=t1时,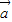 ∥
∥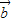 ;t=t2时,
;t=t2时,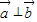 ,则( )
,则( )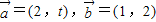 ,若t=t1时,
,若t=t1时,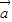 ∥
∥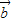 ;t=t2时,
;t=t2时,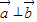 ,则( )
,则( )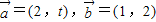 ,若t=t1时,
,若t=t1时,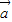 ∥
∥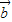 ;t=t2时,
;t=t2时, ,则( )
,则( )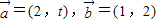 ,若t=t1时,
,若t=t1时,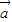 ∥
∥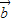 ;t=t2时,
;t=t2时,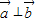 ,则( )
,则( )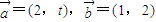 ,若t=t1时,
,若t=t1时,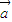 ∥
∥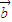 ;t=t2时,
;t=t2时,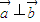 ,则( )
,则( )