题目内容
若平面四边形ABCD满足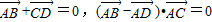
，则该四边形一定是（ ）A．直角梯形
B．矩形
C．菱形
D．正方形
【答案】分析：首先根据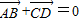
判断出四边形为平行四边形，然后根据
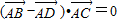证明四边形对角线互相垂直，最后综合以上结论得出四边形为菱形．
解答：解：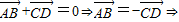
四边形ABCD为平行四边形，
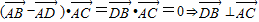
对角线互相垂直的平行四边形为菱形．
故答案为：C
点评：本题考查平面向量与共线向量，以及数量积判断两个向量的垂直关系，需要通过对向量间的关系转化为线段间的关系，然后即可判断四边形的形状．属于基础题．
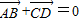判断出四边形为平行四边形，然后根据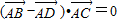证明四边形对角线互相垂直，最后综合以上结论得出四边形为菱形．解答：解：
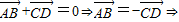
四边形ABCD为平行四边形，
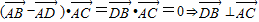
对角线互相垂直的平行四边形为菱形．
故答案为：C
点评：本题考查平面向量与共线向量，以及数量积判断两个向量的垂直关系，需要通过对向量间的关系转化为线段间的关系，然后即可判断四边形的形状．属于基础题．
练习册系列答案
相关题目
若平面四边形ABCD满足
+
=0，(
-
)•
=0，则该四边形一定是（ ）
| AB |
| CD |
| AB |
| AD |
| AC |
| A、直角梯形 | B、矩形 |
| C、菱形 | D、正方形 |
，则该四边形一定是（ ）.
，则该四边形一定是（ ）