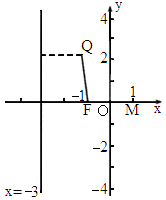题目内容
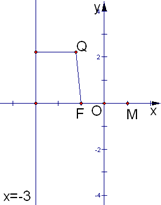
已知点Q位于直线x=-3右侧,且到点F(-1,0)与到直线x=-3的距离之和等于4.(Ⅰ)求动点Q的轨迹C的方程;
(Ⅱ)直线L过点M(1,0)且交曲线C于
A、B两点(A、B不重合),点P满足
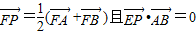 ,其中点E的坐标为(x,0),试求x的取值范围.
,其中点E的坐标为(x,0),试求x的取值范围.
【答案】分析:(Ⅰ)设出点Q,根据两点间的距离公式,依据题意建立等式求得x和y的关系式,整理可知点Q的轨迹抛物线的一部分.
(Ⅱ)设直线L的方程,及A,B的坐标,把直线和抛物线方程联立消去y,根据韦达定理表示出x1+x2和x1x2,进而建立不等式组,求得k的范围,进而根据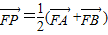 可知,点P为线段AB的中点,P的坐标可知,由
可知,点P为线段AB的中点,P的坐标可知,由 可知,EP⊥AB,分别表示出二者的斜率,其乘积为-1求得x的关于k的表达式,根据k的范围确定x的取值范围.
可知,EP⊥AB,分别表示出二者的斜率,其乘积为-1求得x的关于k的表达式,根据k的范围确定x的取值范围.
解答: 解:(Ⅰ)设点Q(x,y)(x>-3),
解:(Ⅰ)设点Q(x,y)(x>-3),
由题意有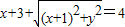 ,
,
整理得y2=-4x,x∈(-3,0]
∴动点Q的轨迹C为以F(-1,0)为焦点,
坐标原点为顶点的抛物线在直线x=-3右侧的部分.
(Ⅱ)由题意可设直线L的方程为y=k(x-1)
设A(x1,y1),B(x2,y2)由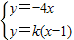 ,
,
得k2x2+(4-2k2)x+k2=0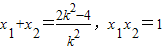 ,
,
由题意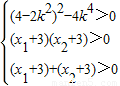 解之得
解之得
由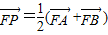 可知,点P为线段AB的中点,∴
可知,点P为线段AB的中点,∴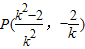 .
.
由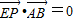 可知,EP⊥AB,∴
可知,EP⊥AB,∴ ,
,
整理得,
∴x的取值范围是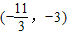
点评:本题主要考查了直线与圆锥曲线的综合问题.解题时应充分发挥判别式和韦达定理在解题中的作用.
(Ⅱ)设直线L的方程,及A,B的坐标,把直线和抛物线方程联立消去y,根据韦达定理表示出x1+x2和x1x2,进而建立不等式组,求得k的范围,进而根据
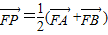 可知,点P为线段AB的中点,P的坐标可知,由
可知,点P为线段AB的中点,P的坐标可知,由 可知,EP⊥AB,分别表示出二者的斜率,其乘积为-1求得x的关于k的表达式,根据k的范围确定x的取值范围.
可知,EP⊥AB,分别表示出二者的斜率,其乘积为-1求得x的关于k的表达式,根据k的范围确定x的取值范围.解答:
 解:(Ⅰ)设点Q(x,y)(x>-3),
解:(Ⅰ)设点Q(x,y)(x>-3),由题意有
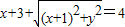 ,
,整理得y2=-4x,x∈(-3,0]
∴动点Q的轨迹C为以F(-1,0)为焦点,
坐标原点为顶点的抛物线在直线x=-3右侧的部分.
(Ⅱ)由题意可设直线L的方程为y=k(x-1)
设A(x1,y1),B(x2,y2)由
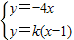 ,
,得k2x2+(4-2k2)x+k2=0
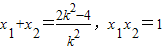 ,
,由题意
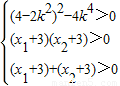 解之得
解之得
由
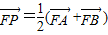 可知,点P为线段AB的中点,∴
可知,点P为线段AB的中点,∴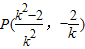 .
.由
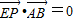 可知,EP⊥AB,∴
可知,EP⊥AB,∴ ,
,整理得,

∴x的取值范围是
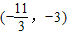
点评:本题主要考查了直线与圆锥曲线的综合问题.解题时应充分发挥判别式和韦达定理在解题中的作用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
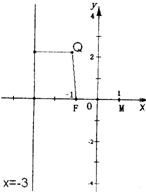 已知点Q位于直线x=-3右侧,且到点F(-1,0)与到直线x=-3的距离之和等于4.
已知点Q位于直线x=-3右侧,且到点F(-1,0)与到直线x=-3的距离之和等于4.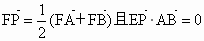 ,其中点E的坐标为(
,其中点E的坐标为(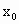 ,0),试求
,0),试求